Contoh Soal Turunan Fungsi Trigonometri
Contoh Soal Turunan Fungsi Trigonometri - Trigonometri merupakan salah satu cabang matematika yang mempelajari sifat-sifat fungsi sinus, kosinus, tangen, kotangen, sekan, dan kosekan berserta aplikasinya untuk menentukan panjang sisi dan ukuran sudut pada segitiga. Sejak berabad-abad yang lalu, trigonometri digunakan secara luas dalam pengukuran dan navigasi. Dalam perkembangannya, para ilmuan banyak memanfaatkan fungsi trigonometri dalam bidang fisika dan astronomi seperti untuk menyatakan gerak benda yang menyerupai gerakan melingkar. Gerakan Bulan mengitari Bumi adalah salah satu contohnya. Dengan fungsi trigonometri, para ahli astronomi dapat menentukan posisi Bulan terhadap Bumi secara pasti.


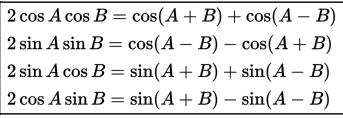
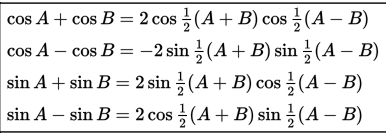
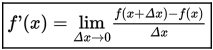




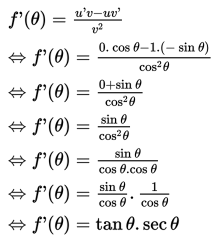
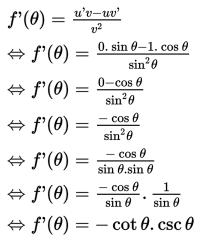
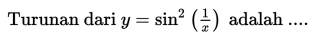

Rumus Jumlah dan Selisih Sudut

Rumus Sudut Rangkap

Rumus Perkalian Sinus dan Kosinus
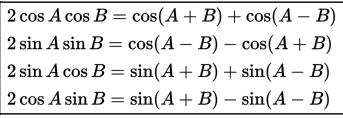
Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus
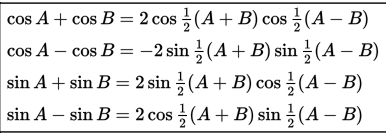
Turunan Dua Fungsi Trigonometri Dasar
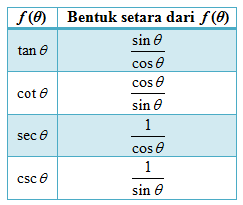
Fungsi sinus dan kosinus dapat dipandang sebagai dua fungsi dasar dalam trigonometri. Hal ini karena untuk fungsi-fungsi trigonometri lainnya seperti tangen, kotangen, sekan, dan kosekan selalu dapat dituliskan kedalam dua fungsi dasar tersebut. Untuk lebih jelasnya, perhatikan tabel berikut.

Turunan dari fungsi sinus dan kosinus dapat ditentukan dengan memanfaatkan definisi turunan. Setelah kita mendapatkan turunan dari dua fungsi dasar ini, selanjutnya akan lebih mudah untuk menentukan turunan dari fungsi trigonometri lainya.
f (x) akan memiliki turunan yang berupa fungsi f ‘ (x) yang didefinisikan sebagai:
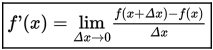
Dengan menggunakan definisi di atas, akan ditentukan turunan dari fungsi sinus dan kosinus.
- Turunan f (θ) = sin θ
Turunan dari f (θ) = sin θ akan ditentukan dengan menggunakan definisi turunan.

Jadi, turunan dari fungsi f (θ) = sin θ adalah f ‘ (θ) = cos θ.
- Turunan g (θ) = cos θ
Turunan dari g (θ) = cos θ akan ditentukan dengan menggunakan definisi turunan.

Jadi, turunan dari fungsi g (θ) = cos θ adalah g ‘ (θ) = -sin θ.
Menentukan Turunan Fungsi Trigonometri Lainnya
Turunan dari fungsi trigonometri tangen, kotangen, sekan, dan kosekan dapat ditentukan dengan memanfaatkan hasil turunan dari fungsi sinus dan kosinus.
- Turunan f (θ) = tan θ
Mula-mula, kita tulis ulang fungsi ini kedalam fungsi dasar trigonometri.
f (θ) = tan θ =
f (θ) = tan θ =
Misalkan u = sin θ dan v = cos θ, sehingga u ‘ = cos θ dan v ‘ = -sin θ.
Dengan menerapkan aturan turunan fungsi rasional (pecahan), maka diperoleh:

Jadi, turunan dari fungsi f (θ) = tan θ adalah f ‘ (θ) = sec2 θ.
- Turunan f (θ) = cot θ
Turunan fungsi f (θ) = cot θ ditentukan dengan cara yang sama dengan penentuan turunan fungsi tangen.
f (θ) = cot θ =
Misalkan u = cos θ dan v = sin θ, sehingga u ‘ = -sin θ dan v ‘ = cos θ.
Dengan menerapkan aturan turunan fungsi rasional (pecahan), maka diperoleh:

Jadi, turunan dari fungsi f (θ) = cot θ adalah f ‘ (θ) = -csc2 θ.
- Turunan f (θ) = sec θ
Turunan fungsi f (θ) = sec θ ditentukan dengan cara yang sama dengan penentuan turunan fungsi tangen dan kotangen.
f (θ) = sec θ =
Misalkan u = 1 dan v = cos θ, sehingga u ‘ = 0 dan v ‘ = -sin θ.
Dengan menerapkan aturan turunan fungsi rasional (pecahan), maka diperoleh:
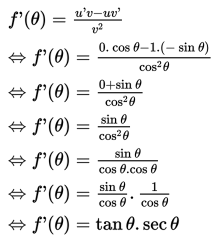
Jadi turunan dari fungsi f (θ) = sec θ adalah f (θ) = tan θ . sec θ.
- Turunan f (θ) = csc θ
f (θ) = csc θ =
Misalkan u = 1 dan v = sin θ, sehingga u ‘ = 0 dan v ‘ = cos θ.
Dengan menerapkan aturan turunan fungsi rasional (pecahan), maka diperoleh:
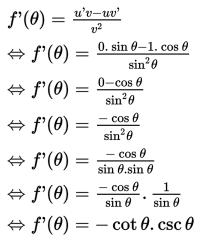
Jadi, turunan dari fungsi f (θ) = csc θ adalah f ‘ (θ) = -cot θ . csc θ.
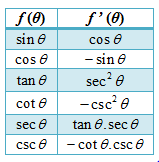
Dari uraian di atas, diperoleh turunan fungsi trigonometri dasar adalah sebagai berikut.

SOAL 1
Bentuk setara dari f (x) = sec x adalah ....
SOAL 2
Jika diketahui f (x) = . maka f ‘ (x) adalah ....
SOAL 3
Turunan pertama dari f (x) = x2 cos x adalah ....
SOAL 4
Turunan pertama dari fungsi y = csc 2θ adalah ....
SOAL 5
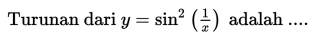
SOAL 6
Turunan pertama dari f (x) = cos3 4x adalah ....
SOAL 7
Apabila f (x) = 2 sin x – 3 cos x, maka nilai dari f ’ (45°) adalah ....
SOAL 8
Apabila f (θ) = cot 3θ, maka nilai dari f ‘ (30°) adalah .…
SOAL 9
Bila f (x) = x + sin 2x, maka nilai dari f ’ (45°) adalah ….
SOAL 10

