Contoh Soal Aplikasi Limit dalam Kehidupan Sehari-Hari
Contoh Soal Aplikasi Limit dalam Kehidupan Sehari-Hari - Limit merupakan suatu konsep yang sangat mendasar dalam matematika khususnya kalkulus (limit, turunan dan integral). Kajiannya yang sangat mendasar membuat penerapannya dalam kehidupan sehari-hari tidak lepas dari ilmu pengetahuan lain seperti kedokteran, fisika dan sebagainya. Mari mengenal dan memahami dengan penuh semangat, penerapan limit dalam kehidupan sehari-hari melalui topik ini. Yuk, kita mulai dengan mengkaji penerapan limit di bidang fisika yaitu masalah kecepatan sesaat.

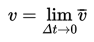
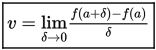

Kamu tentu tidak asing dengan konsep kecepatan rata-rata. Kecepatan rata-rata didefinisikan sebagai perbandingan perpindahan dengan selang waktu . Apabila suatu kendaraan menempuh jarak 50 km dalam waktu 5 jam maka kecepatan rata-rata kendaraan ini adalah 10 km/jam, namun pada kenyataanya kecepatan suatu kendaraan tidaklah berupa besaran yang tetap seperti perhitungan di atas. Hal ini dapat diamati dari kecepatan yang ditunjukan oleh speedometer. Pengereman, tikungan, lampu lalu lintas, kemacetan, dan lain-lain membuat kecepatan suatu kendaraan tidak bisa benar-benar konstan. Konsep kecepatan rata-rata merupakan suatu konsep yang disederhanakan guna mempermudah perhitungan dalam ilmu fisika. Apabila kita hendak menentukan kecepatan suatu benda pada saat tertentu dibutuhkan suatu penjabaran yang lebih rinci yang disebut kecepatan sesaat.Mari simak contoh kecepatan sesaat berikut ini.
Gerak Jatuh Bebas
Posisi suatu benda diudara yang jatuh dari ketinggian h0 (dalam meter) dapat dinyatakan dengan persamaan h (t) = h0 - gt2 dengan g = 10 m/detik2 merupakan percepatan gravitasi di tempat benda jatuh dan t (dalam detik) menyatakan lama benda telah berada di udara. Misalkan suatu benda dijatuhkan dari ketinggian 250 meter dari permukaan tanah, maka setelah t detik benda ini akan berada pada ketinggian h (t) = 250 – 10t2 dengan percepatan gravitasi di tempat itu g = 10 m/detik2 .
Posisi suatu benda diudara yang jatuh dari ketinggian h0 (dalam meter) dapat dinyatakan dengan persamaan h (t) = h0 - gt2 dengan g = 10 m/detik2 merupakan percepatan gravitasi di tempat benda jatuh dan t (dalam detik) menyatakan lama benda telah berada di udara. Misalkan suatu benda dijatuhkan dari ketinggian 250 meter dari permukaan tanah, maka setelah t detik benda ini akan berada pada ketinggian h (t) = 250 – 10t2 dengan percepatan gravitasi di tempat itu g = 10 m/detik2 .
Misalkan kita hendak menentukan kecepatan sesaat benda pada detik pertama benda ini dijatuhkan (t = 1). Kecepatan yang dimaksud dapat dihitung dengan memperkecil selang waktu dalam persamaan kecepatan rata-rata. Perhitungan dari beberapa selang disajikan sebagai berikut.

Apabila perhitungan ini terus dilanjutkan pada selang-selang yang lebih kecil lagi, maka akan diperoleh kecepatan benda saat t = 1. Perhatikan bahwa kita dapat menyatakan kecepatan sesaat dengan mengambil limit dari kecepatan rata-rata untuk selang waktu yang sangat kecil (∆t → 0) yaitu:
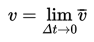
Dengan kata lain, apabila f (t) merupakan fungsi yang menyatakan posisi benda dan δ menyatakan bilangan yang sangat kecil, maka kecepatan sesaat benda pada waktu t = a adalah:
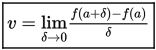
Catatan
Untuk menghindari keraguan, maka penggunaan h pada limit dan definisinya di topik ini diganti dengan δ.
Untuk menghindari keraguan, maka penggunaan h pada limit dan definisinya di topik ini diganti dengan δ.
Dengan demikian, untuk kasus benda jatuh ini kecepatan sesaat benda pada t = 1 adalah:

Tanda negatif dari kecepatan sesaat ini menyatakan arah dari gerak benda karena kecepatan merupakan besaran vektor (besaran yang memiliki nilai dan arah).
SOAL 1
Dalam sesi latihan lari, Ali mampu berlari sejauh 100 meter dalam waktu 5 detik. Kecepatan rata-rata Ali adalah ....
SOAL 2
Posisi suatu benda yang bergerak dinyatakan dengan fungsi s (t) = 15t + 3 meter. Apabila t menyatakan waktu pergerakan benda dalam detik, maka kecepatan rata-rata benda antara t = 1 dan t = 3 detik adalah ....
SOAL 3
Pergerakan seekor semut memenuhi fungsi f (x) = x2 + 3x + 2, dengan x dalam detik dan f (x) dalam cm. Kecepatan gerak semut pada koordinat P (1, 6) adalah ....
SOAL 4
Sebuah partikel bergerak sepanjang kurva y = x2– 1 dengan x dalam detik dan y dalam meter. Kecepatan partikel tersebut di koordinat (2, 3) adalah ....
SOAL 5
Apabila s (t) = 15t + 3 meter menyatakan posisi benda, maka kecepataan benda tersebut setelah t = 3 detik adalah ....
SOAL 6
Disuatu tempat, benda jatuh sejauh 5t2 meter dalam waktu t detik. Kecepatan jatuh benda tersebut saat t = 2 detik adalah ....
SOAL 7
Pertumbuhan modal sebuah perusahaan dinyatakan dalam fungsi M (t) = t2 + 49 juta rupiah, dengan t dalam tahun. Laju pertumbuhan modal perusahaan ini pada tahun ke-3 adalah ....
SOAL 8
Pertambahan massa sel yang membelah dinyatakan dalam fungsi f (t) = t2 + 4 μg dengan t dalam detik (1μg = 0,000001 gram). Laju pertambahan massa sel pada t = 4 detik adalah ....
SOAL 9
Sebuah bola dijatuhkan dari ketinggian 80 meter. Setelah t detik, jarak bola dari tanah dinyatakan dengan fungsi posisi h (t) = 80 – 5t2meter. Kecepatan bola sesaat sebelum bola membentur tanah adalah ....
SOAL 10
Fungsi h (t) = -t2 + 8t meter menyatakan ketinggian kembang api setelah t detik. Ketinggian maksimum yang dapat dicapai oleh kembang api tersebut adalah .…
