Contoh Soal Kekontinuan Fungsi
Contoh Soal Kekontinuan Fungsi - Kekontinuan suatu fungsi dapat dilihat dari grafiknya. Pada kasus benda jatuh bebas, kecepatan benda dapat ditentukan pada sebarang waktu, sedangkan pada kasus saldo tabungan, kita tidak dapat menentukan jumlah saldo pada sebarang waktu tanpa melihat rincian dari transaksi yang telah dilakukan. Penggunaan grafik untuk menentukan kekontinuan fungsi kontinu kurang efisien, sehingga kita memerlukan suatu definisi yang secara tepat menjelaskan tentang kekontinuan fungsi.
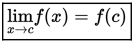

Definisi Kekontinuan Fungsi di Suatu Titik
Misalkan suatu fungsi f (x) terdefinisi pada suatu domain yang meliputi c. f (x) dikatakan kontinu di c apabila:
Misalkan suatu fungsi f (x) terdefinisi pada suatu domain yang meliputi c. f (x) dikatakan kontinu di c apabila:
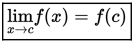
Jika syarat ini tidak terpenuhi, maka f (x) dikatakan diskontinu di c.
Dengan kata lain, definisi kekontinuan fungsi di c ϵ Ɍ tersebut harus memenuhi 3 hal berikut:

Berdasarkan definisi kekontinuan fungsi, diperoleh kekontinuan fungsi-fungsi yang sudah kita kenal sebagai berikut.
• Fungsi suku banyak
Fungsi suku banyak terdefinisi dan kontinu di setiap bilangan real c.
Fungsi suku banyak terdefinisi dan kontinu di setiap bilangan real c.
• Fungsi trigonometri
Fungsi sinus dan cosinus terdefinisi dan kontinu di setiap bilangan real c.
Fungsi sinus dan cosinus terdefinisi dan kontinu di setiap bilangan real c.
• Fungsi rasional (pecahan)
Fungsi rasional terdefinisi dan kontinu di setiap bilangan real c, kecuali titik c yang membuat penyebutnya menjadi nol.
Fungsi rasional terdefinisi dan kontinu di setiap bilangan real c, kecuali titik c yang membuat penyebutnya menjadi nol.
• Fungsi akar pangkat n
Untuk n bilangan ganjil fungsi akar pangkat n terdefinisi dan kontinu di setiap bilangan real c, sedangkan untuk n bilangan genap fungsi terdefinisi dan kontinu disetiap bilangan real positif c.
Untuk n bilangan ganjil fungsi akar pangkat n terdefinisi dan kontinu di setiap bilangan real c, sedangkan untuk n bilangan genap fungsi terdefinisi dan kontinu disetiap bilangan real positif c.
SOAL 1
Diantara kejadian-kejadian berikut, yang merupakan contoh kejadian yang tidak kontinu (diskontinu) adalah ....
SOAL 2
Fungsi f (x) dikatakan kontinu di c apabila ....
SOAL 3
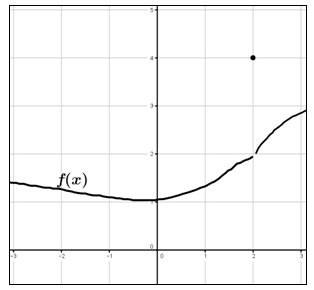
Perhatikan grafik dari suatu fungsi berikut ini. Definisi ulang dari fungsi tersebut menjadi suatu fungsi yang kontinu adalah ....

SOAL 4
Fungsi f (x) = , x ≠ 3 akan menjadi fungsi yang kontinu di x = 3 apabila .
SOAL 5
Nilai x agar f (x) = kontinu adalah ....
SOAL 6
f (x) = akan menjadi fungsi kontinu pada himpunan bilangan real pada saat ....
SOAL 7
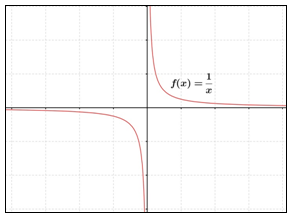
Perhatikan gambar berikut ini. Pernyataan yang salah berkenaan dengan kekontinuan dari f (x) = , x ≠ 0
adalah ....
adalah ....

SOAL 8
Selang terbesar yang membuat fungsi g (x) = kontinu adalah ....
SOAL 9
Nilai θ non-negatif terkecil yang membuat fungsi trigonometri r (θ) = tan (2θ) diskontinu adalah ....
SOAL 10
Misalkan f (x) kontinu dalam interval a ≤ x ≤ b dan terdapat suatu bilangan N yang berada diantara f (a) dan f (b). Pernyataan yang benar diantara pernyataan-pernyataan berikut adalah ....
