Contoh Soal Limit Fungsi Trigonometri

Contoh Soal Limit Fungsi Trigonometri - Pada topik sebelumnya, kalian telah belajar menentukan nilai limit melalui perhitungan nilai-nilai fungsi di sekitar titik limit, yaitu dengan menggunakan teorema limit kiri-limit kanan. Apakah kalian masih ingat? Mari kita ingat kembali teorema tersebut.

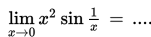
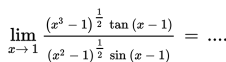
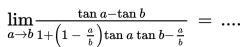
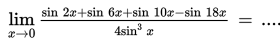
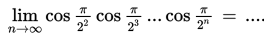
Teorema Limit Kiri-Limit Kanan

Misalkan fungsi f (x) didefinisikan di sekitar x = c, maka limx→cf(x)=L$\underset{x\to c}{lim}f(x)=L$ jika dan hanya jika limx→c−f(x)=L=limx→c+f(x)=L$\underset{x\to c^{-}}{lim}f(x)=L=\underset{x\to c^{+}}{lim}f(x)=L$. limx→c−f(x)=L$\underset{x\to c^{-}}{lim}f(x)=L$ biasa disebut limit kiri dan limx→c+f(x)=L$\underset{x\to c^{+}}{lim}f(x)=L$ biasa disebut limit kanan.

Dengan teorema ini, coba tentukan limx→0sinxx$\underset{x\to 0}{lim}\frac{\text{sin}x}{x}$.

Nilai-nilai f(x)=sinxx$f(x)=\frac{\text{sin}x}{x}$ untuk x mendekati 0 adalah seperti pada tabel berikut.

Dari tabel tersebut, tampak bahwa nilai fungsi f(x)=sinxx$f(x)=\frac{\text{sin}x}{x}$ mendekati 1 jika x mendekati 0 baik dari arah kiri maupun dari arah kanan. Ini berarti limx→0sinxx=1$\underset{x\to 0}{lim}\frac{\text{sin}x}{x}=1$.

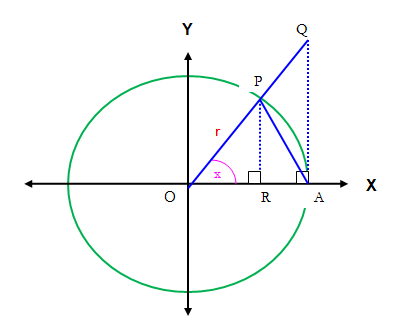
Rumus limx→0sinxx=1$\underset{x\to 0}{lim}\frac{\text{sin}x}{x}=1$ dapat juga kamu buktikan secara geometri seperti berikut.

Coba perhatikan gambar lingkaran yang berpusat di titik O dan berjari-jari r satuan dengan besar ∠AOP = x radian, 0 < x < π2$\frac{\pi }{2}$.

Dari gambar tersebut, pada segitiga OPR didapat PR = r sin x, sedangkan pada segitiga OQA didapat QA = OA . tan x = r tan x.

Luas segitiga OPA < luas juring OPA < luas segitiga OQA.

12$\frac{1}{2}$.OA.PR < 12$\frac{1}{2}$.xr2 < 12$\frac{1}{2}$.OA.QA

r . PR < x . r2 < r . QA

PR < x . r < QA

Mari substitusi PR = r sin x dan QA = r tan x, sehingga didapat:

r sin x < x . r < r . tan x

sin x < x < tan x

Oleh karena 0 < x < π2$\frac{\pi }{2}$, maka sin x > 0. Dengan demikian, kalian dapat membagi ketiga ruas pertidaksamaan dengan sin x tanpa merubah tanda pertidaksamaan.

sinxsinx<xsinx<tanxsinx$\frac{\text{sin}x}{\text{sin}x}<\frac{x}{\text{sin}x}<\frac{\text{tan}x}{\text{sin}x}$

1<xsinx<1cosx$1<\frac{x}{\text{sin}x}<\frac{1}{\text{cos}x}$

Untuk x mendekati 0, pertidaksamaan ini menjadi:

limx→01<limx→0xsinx<limx→01cosx$\underset{x\to 0}{lim}1<\underset{x\to 0}{lim}\frac{x}{\text{sin}x}<\underset{x\to 0}{lim}\frac{1}{\text{cos}x}$

1<limx→0xsinx<1$1<\underset{x\to 0}{lim}\frac{x}{\text{sin}x}<1$

Jadi, nilai limx→0xsinx=1$\underset{x\to 0}{lim}\frac{x}{\text{sin}x}=1$ atau limx→0sinxx=1$\underset{x\to 0}{lim}\frac{\text{sin}x}{x}=1$.

Selain limit fungsi sinus, terdapat pula limit fungsi kosinus, yaitu limx→01−cosxx=0$\underset{x\to 0}{lim}\frac{1-\text{cos}x}{x}=0$ dan limit fungsi tangen, yaitu limx→0tanxx=1$\underset{x\to 0}{lim}\frac{\text{tan}x}{x}=1$.

Limit Fungsi Trigonometri

• limx→0xsinx=1$\underset{x\to 0}{lim}\frac{x}{\text{sin}x}=1$ atau limx→0sinxx=1$\underset{x\to 0}{lim}\frac{\text{sin}x}{x}=1$
• limx→0tanxx=1$\underset{x\to 0}{lim}\frac{\text{tan}x}{x}=1$ atau limx→0xtanx=1$\underset{x\to 0}{lim}\frac{x}{\text{tan}x}=1$
• limx→01−cosxx=0$\underset{x\to 0}{lim}\frac{1-\text{cos}x}{x}=0$

SOAL 1

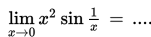
SOAL 2

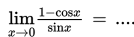
SOAL 3

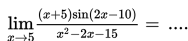
SOAL 4

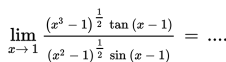
SOAL 5

Jika fungsi f (x) = sin x + cos x,

maka limx→cf(x)−f(c)x−c$\underset{x\to c}{lim}\frac{f(x)-f(c)}{x-c}$ = ....

SOAL 6

Jika fungsi g (x) = 3 cos 2x,

maka limh→0g(x+h)−g(x)h$\underset{h\to 0}{lim}\frac{g(x+h)-g(x)}{h}$ = ....

SOAL 7

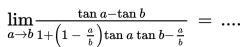
SOAL 8

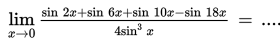
SOAL 9

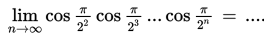
SOAL 10

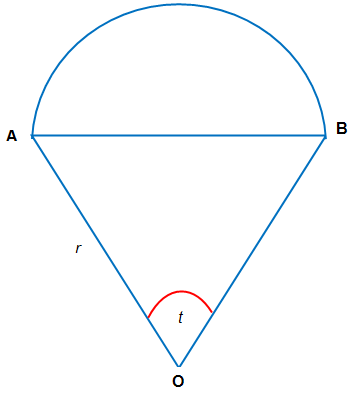
Sebuah segitiga samasisi dengan panjang sisi r ditutup oleh setengah lingkaran seperti pada gambar berikut.

Jika D luas segitiga AOB dan E luas setengah lingkaran tersebut, maka limx→𝛑2ED$\underset{x\to \frac{𝛑}{2}}{lim}\frac{E}{D}$ = ....

Share this post