Contoh Soal Syarat Kekongruenan Segitiga

Contoh Soal Syarat Kekongruenan Segitiga - Mari simak ilustrasi berikut.

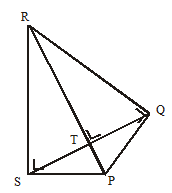
Gambar di atas adalah susunan ubin yang terdiri dari segitiga–segitiga yang memiliki bentuk dan ukuran yang sama. Pemasangan ubin-ubin tersebut menggunakan salah satu konsep matematika yaitu kekongruenan. Dua segitiga atau lebih dikatakan kongruen (sama dan sebangun) jika bentuk dan ukuran segitiga-segitiga tersebut sama. Jika dilakukan pergeseran atau pemutaran salah satu pasangan segitiga kongruen terhadap segitiga yang lain, maka segitiga tersebut akan tepat menempati segitiga kongruen pasangannya. Kongruen dilambangkan dengan $\cong$, sehingga jika terdapat dua buah segitiga yang kongruen misalnya ΔABC kongruen dengan ΔPQR, maka dapat ditulis sebagai $\Delta ABC\cong \Delta PQR$.

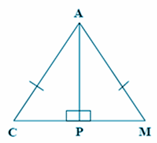
Perhatikan gambar berikut.

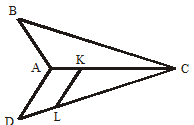
Dari gambar di atas diketahui bahwa ΔACM adalah segitiga sama kaki. Sisi AP merupakan garis tinggi ΔACM, sehingga membentuk ΔACP dan ΔAMP. Apakah ΔACP kongruen dengan ΔAMP? ΔACP kongruen dengan ΔAMP (ΔACP ≅ ΔAMP) karena:

• ΔACP dapat tepat menempati ΔAMP dengan cara mencerminkan ΔACP terhadap garis AP atau semua sisi ΔACP memiliki panjang yang sama dengan ΔAMP.
• ΔCAM merupakan segitiga sama kaki, sehingga ∠ACP = ∠AMP (sudut pada kaki segitiga samakaki ΔCAM) dan ∠APC = ∠APM = 90⁰. Ini berakibat ∠CAP = ∠MAP.

Dari uraian di atas diperoleh kesimpulan sebagai berikut.

Sifat-Sifat Dua Segitiga yang Kongruen

• Sisi–sisi yang bersesuaian mempunyai panjang yang sama
• Sudut–sudut yang seletak besarnya sama

Syarat-Syarat Dua Segitiga yang Kongruen

• Dua segitiga akan kongruen jika ketiga sisi yang bersesuaian dari dua segitiga itu sama panjang (s, s, s).

       Perhatikan jajargenjang PQRS. Garis QS merupakan diagonal jajargenjang PQRS yang membaginya menjadi 2 buah segitiga yaitu ΔPQS dan ΔRSQ. Apakah ΔPQS kongruen dengan ΔRSQ? Pada jajargenjang PQRS, sisi-sisi yang berhadapan sejajar dan sama panjang yaitu:

PQ // SR sehingga PQ = SR
PS // QR sehingga PS = QR.

Selanjutnya, QS adalah diagonal bidang sehingga QS = SQ. Dengan demikian, sisi-sisi yang bersesuaian dari ΔPQS dan ΔRSQ sama panjang. Jadi, ΔPQS dan ΔRSQ kongruen.

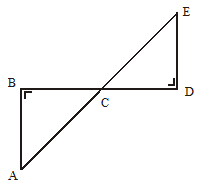
• Dua segitiga akan kongruen jika dua sisi pada segitiga pertama sama panjang dengan dua sisi yang bersesuaian pada segitiga kedua, dan besar sudut apit dari kedua sisi tersebut sama (s, sd, s).

       Pada gambar tersebut, sisi DE = KL, ∠D = ∠K, dan DF = KM. Jika kita mengukur panjang sisi dan besar sudut lainnya yaitu sisi EF dan LM, ∠E dan ∠L, serta ∠F dan ∠M, maka akan diperoleh:

EF = LM
∠E = ∠L
∠F = ∠M.

Dengan demikian, pada ΔDEF dan ΔKLM berlaku panjang DE = KL, EF = LM, dan DF = KM. ini berati bahwa pada ΔDEF dan ΔKLM sisi-sisi yang bersesuaian sama panjang. Selain itu, besar ∠D = ∠K, ∠E = ∠L, dan ∠F = ∠M. Ini berarti bahwa sudut-sudut yang bersesuaian sama besar. Hal ini menunjukkan bahwa ΔDEF dan ΔKLM memenuhi sifat dua segitiga yang kongruen.

• Dua segitiga akan kongruen jika dua sudut pada segitiga pertama sama besar dengan dua sudut yang bersesuaian pada segitiga kedua, dan sisi yang merupakan kaki persekutuan kedua sudut sama panjang (sd, s, sd).

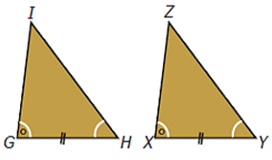
       Pada gambar tersebut, ∠G = ∠X, ∠H = ∠Y, dan sisi GH = XY. Jika kita mengukur besar ∠I dan ∠Z, panjang sisi GI dan XZ, serta panjang HI dan YZ, maka akan diperoleh:

besar ∠I = ∠Z
panjang sisi GI = XZ
panjang HI = YZ.

Dengan demikian, pada ΔGHI dan ΔXYZ berlaku, ∠G = ∠X, ∠H = ∠Y, dan ∠I = ∠Z. Ini berati bahwa pada ΔGHI dan ΔXYZ sudut-sudut yang bersesuaian sama besar. Panjang GH = XY, HI = YZ, dan GI = XZ. Ini berarti bahwa pada ΔGHI dan ΔXYZ sisi-sisi yang bersesuaian sama panjang. Hal ini menunjukkan bahwa ΔGHI dan ΔXYZ memenuhi sifat dua segitiga yang kongruen.

Perbedaan antara Kesebangunan dan Kekongruenan pada Segitiga

✎Contoh 1

Perhatikan gambar berikut.

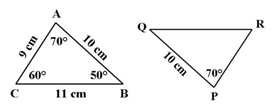
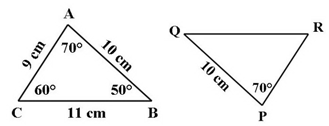
Jika ΔABC kongruen dengan ΔPQR, maka tentukan:
- panjang PR
- panjang QR
- ∠PQR
- ∠QRP

Penyelesaian:

• Oleh karena sisi PR bersesuaian dengan AC, maka panjang sisi PR = AC = 9 cm.
• Oleh karena sisi QR bersesuaian dengan CB, maka panjang QR = CB = 11 cm.
• Oleh karena ∠PQR bersesuaian dengan ∠ABC, maka ∠PQR = ∠ABC = 50⁰.
• Oleh karena ∠QRP bersesuaian dengan ∠ACB, maka ∠ QRP = ∠ ACB = 60⁰.

S1

Pernyataan berikut ini yang benar adalah .…

S2

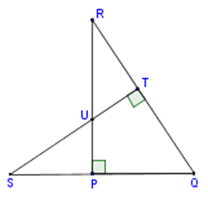
Perhatikan gambar berikut.

Jika panjang sisi PQ = QT, maka syarat yang dipenuhi sehingga ΔPQR kongruen dengan ΔTQS adalah ….

S3

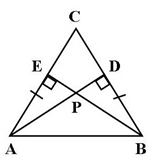
Perhatikan gambar berikut.

Diketahui segitiga samakaki ABC dengan sisi AB sebagai alas. Jika AD dan BE adalah garis tinggi yang tegak lurus sisi BC dan AC, serta berpotongan di titik P, maka banyak pasangan segitiga yang kongruen adalah … buah.

S4

Perhatikan gambar berikut.

Jika segitiga ABC kongruen dengan segitiga PQR, maka panjang sisi QR, besar ∠PQR, dan besar ∠PRQ berturut-turut adalah ….

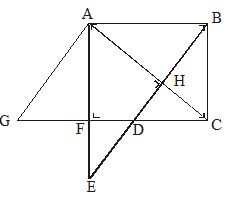
S5

Perhatikan gambar berikut. Jika ABDG adalah belahketupat, maka pasangan segitiga yang kongruen adalah ….

S6

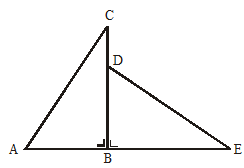
Perhatikan gambar di bawah ini.
Jika ΔABC $\cong$ ΔDBE, panjang sisi BC = 12 cm, dan CD = $\frac{1}{3}$DB, maka panjang DE adalah ....

S7

Diketahui segitiga samakaki ACM dengan panjang AC = AM = 25 cm dan CM = 14 cm. Jika ΔACM kongruen dengan ΔRQN, maka luas segitiga RQN adalah … cm2 .

S8

Pada gambar di bawah ini, ΔABC $\cong$ ΔADC, panjang AC = 12 cm, KL = 4 cm, dan KC = 6 cm. Jika AD //KL dan ∠DAC = ∠BAC, maka panjang AB adalah ... cm.

S9

Bangun PQRS dibentuk dari dua segitiga yang kongruen, yaitu ΔPSR dan ΔPQR. Jika SQ = 12 cm dan RT = 8 cm, serta ΔRST sebangun dengan ΔSPT, maka keliling PQRS adalah … cm.

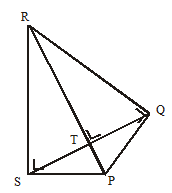
S10

Pada gambar berikut, diketahui ΔABC kongruen dengan ΔEDC. Jika panjang AE = 10 cm, luas segitiga ABC = 6 cm2 , dan sisi BC lebih panjang daripada AB, maka panjang sisi ED adalah … cm

Share this post