Contoh Soal Penerapan Kekongruenan dan Kesebangunan dalam Kehidupan Nyata
Contoh Soal Penerapan Kekongruenan dan Kesebangunan dalam Kehidupan Nyata - Pada topik sebelumnya, kamu telah mempelajari sifat-sifat kesebangunan bangun datar, yaitu sebagai berikut.





Sifat-sifat tersebut akan kita terapkan untuk menyelesaikan masalah sehari-hari seperti berikut ini.
⚽ Ayo Memahami!
Sebelum membangun sebuah lapangan sepakbola berskala internasional, seorang arsitek terlebih dahulu membuat miniatur dari lapangan tersebut. Miniatur ini bentuknya sama dengan bentuk lapangan yang akan dibangun dengan ukuran yang diperkecil.
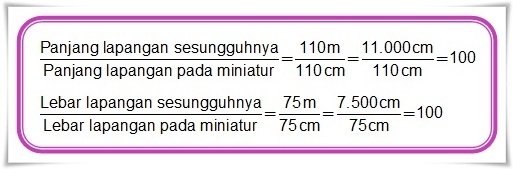
Setelah lapangan tersebut selesai dibangun, sang arsitek mengukur panjang dan lebar lapangan. Ia mendapatkan panjang dan lebar lapangan berturut-turut 110 m dan 75 m. Kemudian, ia membandingkannya dengan ukuran pada miniatur. Pada miniatur, lapangan tersebut memiliki panjang 110 cm dan lebar 75 cm.
Coba kamu perhatikan perbandingan ukuran lapangan sepakbola sesusungguhnya dengan ukuran pada miniatur.

Jadi, perbandingan panjang dan lebar lapangan sepakbola sesungguhnya dengan panjang dan lebar lapangan pada miniatur adalah 100 : 1. Begitu pula dengan perbandingan bagian-bagian lainnya, seperti tinggi tiang gawang, pasti akan didapatkan perbandingan 100 : 1.
Dari uraian ini, kamu dapat mengetahui bahwa:

Sekarang, coba amati bentuk lapangan sepakbola.
Lapangan sepakbola berbentuk persegipanjang sehingga setiap sudutnya berukuran 90°. Begitu juga dengan lapangan sepakbola pada miniatur, berbentuk persegipanjang sehingga besar sudutnya 90°.
Dari uraian ini, kamu dapat mengetahui bahwa:

Berdasarkan dua hal ini dapat disimpulkan bahwa lapangan sepakbola sebangun dengan miniaturnya.
🎱 Penerapan Kekongruenan
Pada topik sebelumnya, kamu telah mempelajari sifat-sifat kekongruenan bangun datar, yaitu sebagai berikut.

Jika salah satu dari syarat tersebut tidak dipenuhi maka dua bangun dikatakan tidak kongruen.
Sifat-sifat tersebut akan kita terapkan untuk menyelesaikan masalah sehari-hari seperti berikut ini.
📖 Ayo Memahami!
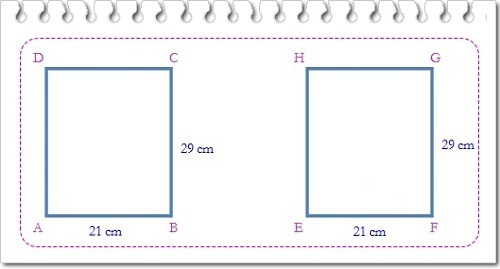
Lembaran kertas dalam buku berbentuk persegipanjang dengan ukuran panjang 29 cm dan lebar 21 cm. Misalnya, kita ambil dua lembar kertas berbentuk persegipanjang ABCD dan EFGH seperti berikut.

Coba amati panjang sisi-sisi yang bersesuaian pada kedua persegipanjang tersebut.
📌 AB = EF = 21 cm 📌 DC = HG = 21 cm
📌 BC = FG = 29 cm 📌 AD = EH = 29 cm
Ternyata, sisi-sisi yang bersesuaian sama panjang.
Coba amati pula besar sudut-sudut yang bersesuaian pada kedua persegipanjang tersebut.
Pada persegipanjang, keempat sudutnya merupakan sudut siku-siku sehingga sudut-sudut yang bersesuaian antara dua persegipanjang tersebut adalah sama besar.
Berdasarkan dua hal ini dapat disimpulkan bahwa persegipanjang ABCD dan EFGH tersebut menunjukkan lembaran kertas yang kongruen.
S1
Sebuah gedung memiliki bayangan sepanjang 20 m. Pada saat yang sama, Alfarabi yang berada di dekat gedung tersebut memiliki bayangan sepanjang 2 m. Jika tinggi Alfarabi 1,7 m, tinggi gedung tersebut adalah ….
S2
Di antara benda-benda berikut yang sebangun dengan halaman buku gambar berukuran 21 cm x 15 cm adalah …
S3
Sebuah tiang bendera setinggi 6 m berdiri tegak di samping sebuah menara. Panjang bayangan tiang bendera 1,5 m dan panjang bayangan menara 18 m. Tinggi menara tersebut adalah … m.
S4
Kevin Tara mempunyai dua koin yang berbentuk lingkaran. Jari-jari koin pertama 7 cm. Jika perbandingan luas koin pertama dengan koin kedua 1 : 9, maka panjang jari-jari koin kedua adalah … cm.
S5
Sejengkal tanah berukuran 24 m x 20 m. Ketika digambar pada selembar kertas, ukurannya adalah 6 cm x 5 cm. Skala gambar tersebut adalah ….
S6
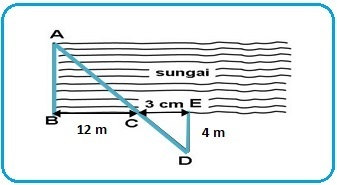
Seorang pemuda menghitung lebar sungai dengan menancapkan tongkat di B, C, D, dan E (seperti pada gambar) sehingga DCA segaris (A = benda di seberang sungai). Lebar sungai (AB) adalah ….

S7
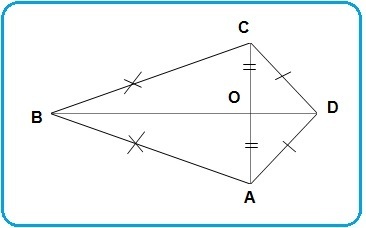
Kevin Tara jago bermain layang-layang. Selain itu, ia juga jago dalam membuatnya. Berikut ini layang-layang yang dibuat Kevin Tara jika dinyatakan dalam bentuk bangun datarnya.

Pernyataan yang salah adalah ….
S8
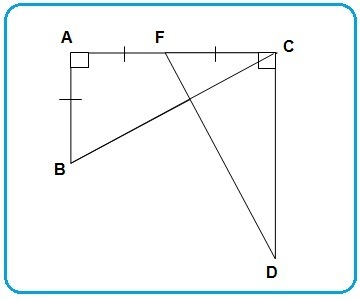
Kevin Tara memiliki dua buah penggaris segitiga. Misalkan kedua penggaris segitiga itu dinamainya ABC dan CDF. Setiap huruf digunakan untuk menyatakan titik sudutnya. Kedua penggaris tersebut disusunnya sebagai berikut.

Diketahui ∠ABC = ∠DFC, titik F merupakan titik tengah AC, panjang AC = 2AB, dan AC = CD. Dikatakan bahwa ∆ABC ≅ ∆CDF karena hal-hal berikut, kecuali ….
S9
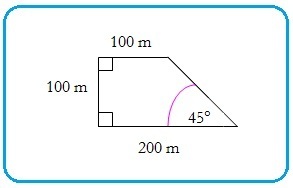
Berikut ini adalah sketsa tambak udang milik Pak Windu yang berbentuk trapesium siku-siku.

Pak Windu akan membagi tambaknya tersebut menjadi empat bagian yang kongruen. Luas setiap bagian adalah … m2 .
S10
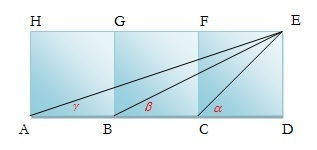
Tiga buah jendela kaca berbentuk persegi yang kongruen disusun seperti berikut.

Jika seberkas sinar masuk dari titik sudut E, maka dapat dibuktikan bahwa ….
