Contoh Soal Momentum Sudut dalam Dinamika Rotasi
Contoh Soal Momentum Sudut dalam Dinamika Rotasi - Pada topik sebelumnya, kalian telah belajar tentang momen inersia dan kecepatan sudut dalam materi kesetimbangan benda tegar. Pada topik ini, kalian akan belajar tentang topik momentum sudut dalam dinamika rotasi. Untuk mempelajarinya lebih lanjut, simak ulasan berikut.
A. Momentum Sudut (Momentum Angular)
Jika sebuah partikel yang memiliki massa bergerak dengan kecepatan v, maka partikel tersebut dikatakan memiliki momentum. Dalam gerak linear (gerak lurus) kalian telah mengenal momentum linear p = mv, sedangkan pada gerak rotasi kalian mengenal besaran momentum sudut (L). Apa itu momentum sudut? Momentum sudut didefinisikan sebagai hasil perkalian antara momen inersia dan kecepatan sudut partikel. Secara matematis, dirumuskan sebagai berikut.
atau
Keterangan:
L = momentum sudut (kg.m2/s),
I = momen inersia (kg.m2),
ω = kecepatan sudut (rad/s);
m = massa benda (kg);
v = kecepatan linear (m/s); dan
R = jarak titik ke sumbu putar (m).
L = momentum sudut (kg.m2/s),
I = momen inersia (kg.m2),
ω = kecepatan sudut (rad/s);
m = massa benda (kg);
v = kecepatan linear (m/s); dan
R = jarak titik ke sumbu putar (m).
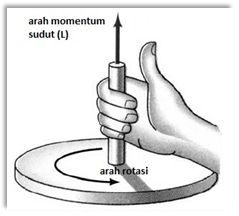
Dalam gerak rotasi, momen inersia dapat dianalogikan dengan massa (m) dan kecepatan sudut (ω) dapat dianalogikan dengan kecepatan linear (v). Momentum sudut merupakan besaran vektor seperti pada momentum linear, dimana arah dari momentum sudut dapat ditentukan dengan aturan tangan kanan, yaitu putar keempat jari yang dirapatkan sesuai dengan arah gerak rotasi. Arah ibu jari menyatakan arah vektor momentum sudut.

B. Hukum Kekekalan Momentum Sudut
Seperti pada gerak linear (gerak lurus) yang berlaku hukum kekekalan momentum, pada gerak rotasi juga berlaku adanya hukum kekekalan momentum sudut, yaitu jika resultan momen gaya luar yang bekerja pada sistem nol (Στ = 0), maka jumlah total momentum sudut sistem tetap/ kekal baik besar dan arahnya. Secara matematis, hukum kekekalan momentum sudut dirumuskan sebagai berikut.
atau
Keterangan:
L1 = momentum sudut mula-mula;
L2 = momentum sudut akhir;
I1 = momen inersia mula-mula;
I2 = momen inersia akhir;
ω1 = kecepatan sudut mula-mula; dan
ω2 = kecepatan sudut akhir.
L1 = momentum sudut mula-mula;
L2 = momentum sudut akhir;
I1 = momen inersia mula-mula;
I2 = momen inersia akhir;
ω1 = kecepatan sudut mula-mula; dan
ω2 = kecepatan sudut akhir.
Penerapan hukum kekekalan momentum sudut terlihat pada gerakan penari es (skater) dan pelompat indah.
a. Seorang penari es akan berputar lebih cepat dengan cara melipat kedua lengannya di dekat badan dan sebaliknya. Penari tersebut akan berputar lebih lambat saat merentangkan kedua lengannya.
b. Seorang pelompat indah akan menekuk tubuhnya ketika melakukan putaran di udara dan pada tahap akhir lompatannya, pelompat memanjangkan tubuhnya sehingga ia dapat terjun ke air dengan kecepatan lebih rendah.
b. Seorang pelompat indah akan menekuk tubuhnya ketika melakukan putaran di udara dan pada tahap akhir lompatannya, pelompat memanjangkan tubuhnya sehingga ia dapat terjun ke air dengan kecepatan lebih rendah.
SOAL 1
Sebuah bola bergerak di permukaan meja dengan lintasan berbentuk lingkaran. Bola tersebut berjari-jari r dengan kecepatan sudut konstan. Pernyataan berikut ini berkaitan dengan momentum linear dan momentum sudut bola.
(1). Momentum linear konstan.
(2). Momentum sudut konstan.
(3). Momentum sudut berubah.
(4). Momentum linear berubah.
(2). Momentum sudut konstan.
(3). Momentum sudut berubah.
(4). Momentum linear berubah.
Pernyataan yang benar ditunjukkan oleh nomor ....
SOAL 2
Seorang penari es memperlambat kecepatan putarannya dengan merentangkan lengan tangan dari sumbu putarnya. Hal ini dikarenakan ....
SOAL 3
Sebuah bola pejal mempunyai massa 600 gr dan jari-jari 10 cm. Bola tersebut diputar pada sumbu yang melalui pusat bola dengan kecepatan sudut 400 rpm. Momentum sudut bola pejal tersebut adalah ...
SOAL 4
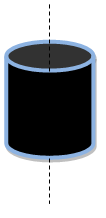
Sebuah silinder pejal berotasi dengan kecepatan sudut 5 rad/s seperti gambar berikut.

Jika silinder pejal memiliki massa 3 kg dan jari-jari 0,1 m, maka besar momentum sudutnya adalah ....
SOAL 5
Seorang penari es memiliki momen inersia 4 kg.m2 dan kecepatan sudut 1,8 putaran/s saat kedua lengan terentang. Ketika kedua lengan merapat, momen inersianya menjadi 1,2 kg.m2. Kecepatan sudut ketika kedua lengan merapat adalah ....
SOAL 6
Sebuah benda bermassa 2 kg terletak pada jarak 1 m dari sumbu putar piringan yang bermassa 100 kg dan jari-jari 1 m. Benda tersebut berotasi dengan kecepatan sudut 5 rad/s. Jika benda secara perlahan-lahan dipindahkan ke posisi 0,5 m dari sumbu rotasi, maka kecepatan sudut akhirnya adalah ....
SOAL 7
Momentum sudut memiliki besar dan arah, sehingga momentum sudut termasuk jenis besaran ....
SOAL 8
Untuk menentukan arah dari momentum sudut, kalian dapat menggunakan aturan tangan kanan yaitu ....
SOAL 9
Contoh penerapan hukum kekekalan momentum sudut yang tepat dalam kehidupan sehari-hari adalah ....
SOAL 10
Pernyataan hukum kekekalan momentum sudut adalah ....
