Contoh Soal Menentukan Kedudukan Dua Garis
Contoh Soal Menentukan Kedudukan Dua Garis - Pada topik sebelumnya, kalian telah belajar tentang letak titik terhadap garis dan persamaan garis sederhana. Dalam sistem koordinat Cartesius, kalian telah mampu menggambar garis dan menentukan persamaannya. Kalian juga dapat melihat bahwa setiap garis mempunyai hubungan tertentu dengan garis-garis yang lain. Coba perhatikan hubungan garis-garis berikut.
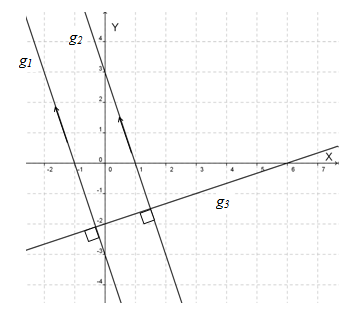
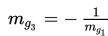
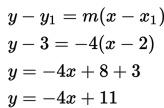

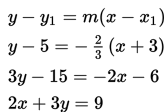
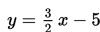
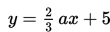
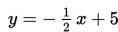
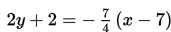
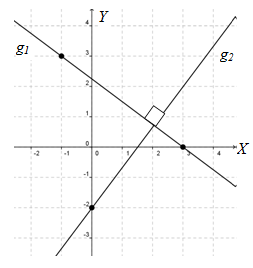

Nampak bahwa garis g1 sejajar dengan g2, dan g1 maupun g2 tegak lurus dengan garis g3.
Berdasarkan gambar, nampak bahwa garis g1 melalui titik (-1 , 0) dan (0 , -3). Dengan demikian, persamaan garis g1 adalah -3x - y= 3 dan gradien garis g1 adalah –3 atau mg1 = - 3.
Nah, berdasarkan gambar di atas pula, nampak bahwa garis g2 melalui titik (1,0) dan (0,3). Dengan demikian, persamaan garis g2adalah 3x + y = 3 dan gradien garis g2 adalah –3 atau mg2 = - 3.
Nah, apa yang dapat kalian simpulkan dari fakta ini?
Dari dua fakta tersebut diperoleh garis g1 sejajar dengan g2 dan mg1 = mg2
Sekarang perhatikan garis melalui titik (6,0) dan (0,-2) maka dapat ditentukan persamaan garis g3 yaitu x – 3y = 6. Gradien garis ini adalah 1/3 atau mg3 = 1/3.
Apa yang dapat kalian simpulkan tentang gradien garis g3 dengan g1 dan g3?
Apa yang dapat kalian simpulkan tentang gradien garis g3 dengan g1 dan g3?
Garis g3 tegak lurus dengan garis g1 dan mg1mg3 = - 1 atau
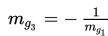
Dari semua contoh dan penjelasan di atas dapat kita simpulkan hubungan antara dua garis adalah:
1) Garis g dan garis h sejajar maka mg = mh
2) Garis g tegak lurus dengan garis h maka mgmh = - 1
1) Garis g dan garis h sejajar maka mg = mh
2) Garis g tegak lurus dengan garis h maka mgmh = - 1
Agar lebih jelas perhatikan contoh berikut ini
Contoh 1:
Tentukan persamaan garis melalui titik (2,3) dan sejajar garis y = -4x + 5
Penyelesaian:
Diketahui bahwa jika dua garis sejajar maka gradien (kemiringan garis) sama.
Gradien garis y = -4x + 5 adalah m = -4
Maka selanjutnyayang akan kita lakukan adalah menentukan persamaan garis melalui titik (2,3) dengan gradien m = -4.
Gradien garis y = -4x + 5 adalah m = -4
Maka selanjutnyayang akan kita lakukan adalah menentukan persamaan garis melalui titik (2,3) dengan gradien m = -4.
Persamaannya adalah
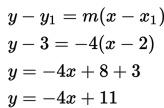
Jadi persamaan garis melalui titik (2,3) dengan gradien m = -4 adalah y = -4x + 11
Contoh 2:
Tentukan persamaan garis yang melalui titik (-3,5) dan tegak lurus dengan garis 6x – 4y – 5 = 0
Penyelesaian:
Gradien garis 6x – 4y – 5 = 0 adalah m = 3/2 yang selanjutnya kita sebut m1 = 3/2.
Gradien garis yang akan dicari kita sebut m2.
Dua garis dengan gradien m1 dan m2 saling tegak lurus jika m1.m2 = -1, maka
Gradien garis yang akan dicari kita sebut m2.
Dua garis dengan gradien m1 dan m2 saling tegak lurus jika m1.m2 = -1, maka

Maka langkah berikutnya adalah menentukan persamaan garis melalui titik (-3,5) dengan gradien m = - 2/3
Persamaannya adalah
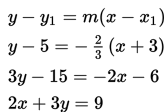
Jadi persamaan garis yang melalui titik (-3,5) dan tegak lurus dengan garis 6x – 4y – 5 = 0 adalah 2x + 3y = 9
S1
Garis g sejajar dengan garis
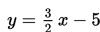
maka gradien garis g adalah ….
S2
Garis k tegak lurus dengan garis 6x – 2y = 7, maka gradien garis k adalah ….
S3
Garis h melalui titik (0,5) dan sejajar dengan sumbu x, maka gradien garis h adalah ….
S4
Garis ax + 4y = 6 sejajar dengan garis 9x + ay = 8, maka nilai a adalah ….
S5
Garis
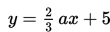
tegak lurus dengan garis
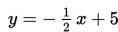
maka nilai a sama dengan ….
S6
Persamaan garis yang melalui titik (2,7) dan sejajar dengan garis 5x – 2y = 8 adalah ….
S7
Persamaan garis melalui titik (-3,-2) dan tegak lurus dengan garis
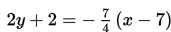
adalah ….
S8
Diketahui garis g melalui titik (-2,6) dan (8,8). Jika garis h melalui titik (8,8) dan sejajar dengan g, maka persamaan garis h adalah ….
S9
Garis g melalui titik (3,8) dan sejajar sumbu y.
Garis h melalui titik (4,-5) dan tegak lurus garis g.
Persamaan garis h adalah ….
Garis h melalui titik (4,-5) dan tegak lurus garis g.
Persamaan garis h adalah ….
S10
Perhatikan gambar garis berikut

Diketahui garis g1 tegak lurus dengan garis g2, persamaan garis g2 adalah ….
