Contoh Soal Penerapan Barisan dan Deret Geometri dalam Kehidupan Sehari-Hari

Contoh Soal Penerapan Barisan dan Deret Geometri dalam Kehidupan Sehari-Hari - Dalam kehidupan sehari-hari, selain permasalahan yang dapat diselesaikan dengan menggunakan konsep barisan dan deret aritmetika, juga terdapat permasalahan yang dapat diselesaikan dengan memanfaatkan konsep barisan dan deret geometri. Ayo cari tahu variasi permasalahan dan penyelesaiannya dengan mempelajari topik ini.

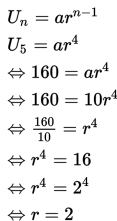
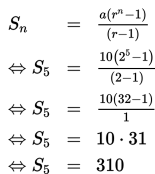
       Agar kamu mahir dalam menyelesaikan masalah barisan dan deret geometri, mari ingat kembali tentang konsep barisan dan deret geometri. Pada topik-topik sebelumnya telah dijelaskan bahwa suatu barisan bilangan U1 , U2 , U3 , ... , Un disebut barisan geometri, jika untuk tiap bilangan asli n berlaku:

$\frac{U_n}{U_{n-1}}=r$

Dengan, 
Un = suku ke-n
Un - 1 = suku ke-(n - 1) 
r = rasio atau perbandingan

Suku ke-n dari suatu barisan geometri ditentukan melalui rumus:

$U_n=a{r}^{n-1}$

Dengan a = U1 = suku pertama, r = rasio atau perbandingan dan n = banyak suku.

Jika U1 , U2 , U3 , ... , Un adalah suku-suku barisan geometri, maka U1 + U2 + U3 + ... + Un disebut deret geometri. Jadi, suku-suku dari suatu deret geometri berasal dari barisan geometri. Bentuk umum untuk deret geometri, yaitu
a + ar + ar2 + ar3 + ... + arn-1

Untuk menghitung jumlah n suku pertama suatu deret geometri digunakan rumus sebagai berikut:

• Deret naik, $S_n=\frac{a(r^n-1)}{r-1}$ untuk r > 1 dan r ≠ 1

• Deret turun, $S_n=\frac{a(1-r^n)}{1-r}$ untuk r < 1 dan r ≠ 1

        Kita telah mengingat kembali tentang barisan dan deret geometri, lalu bagaimana cara menerapkan konsep tersebut dalam pemecahan masalah? Berikut ini akan diberikan beberapa contoh mengenai penerapan konsep barisan dan deret geometri dalam kehidupan sehari-hari.

Contoh 1

Seutas tali dibagi menjadi 5 bagian yang panjangnya membentuk barisan geometri. 
Jika tali yang paling pendek adalah 10 cm dan tali yang paling panjang adalah 160 cm, tentukan panjang tali semula.

Penyelesaian:

Diketahui potongan-potongan tali membentuk barisan geometri, dengan: 
panjang tali terpendek = U1 = a = 10
panjang tali terpanjang = U5 = ar4 = 160
banyak bagian tali = n = 5

Ini berarti panjang tali semula adalah jumlah panjang kelima bagian tali (S5).

Mula-mula tentukan nilai r dengan mengganti a = 10, n = 5 dan U5 = 160 ke rumus Un.

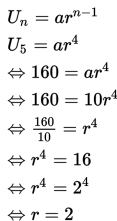
Selanjutnya tentukan panjang panjang tali semula (S5) yaitu

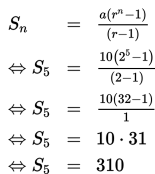
Jadi, panjang tali semula adalah 310 cm.

S1

Panitia suatu acara terdiri atas 3 tim yaitu tim A, B dan C. Banyak angggota masing-masing tim berturut-turut membentuk barisan geometri. Banyak anggota tim B dua kali anggota tim A dan tim C dua kali tim B. Jika tim A beranggotakan 6 orang, maka jumlah seluruh anggota panitia adalah ....

S2

Seseorang berlari dengan kecepatan 16 km/jam selama 1 jam pertama. Pada jam kedua kecepatan berkurang menjadi seperduanya, demikian juga pada jam berikutnya, kecepatan menjadi seperdua dari sebelumnya. Total jarak yang ditempuh orang itu setelah 3 jam berlari adalah....

S3

Sebuah peternakan terkena wabah virus flu burung. Pada hari pertama terdapat 2.430 ekor ayam yang masih hidup. Pada hari kedua, banyak ayam yang masih hidup berkurang menjadi sepertiganya. Kejadian yang sama terus berulang di hari-hari berikutnya. Banyak ayam yang tersisa pada hari kelima adalah ....

S4

Seutas tali dibagi menjadi 6 bagian dengan panjang membentuk barisan geometri. Jika tali yang paling pendek adalah 8 cm dan tali yang paling panjang adalah 256 cm, panjang tali semula adalah ….

S5

Diva memiliki seutas tali rafia sepanjang 160 cm. Tali rafia tersebut ia potong menjadi beberapa bagian sehingga panjang masing-masing potongannya membentuk barisan geometri. Jika panjang potongan rafia terpendek adalah 4 cm dan rasio antar potongannya 3, maka banyaknya potongan rafia adalah ....

S6

Raffi baru saja membeli buku bacaan baru setebal 1.022 halaman. Jika Raffi memiliki target membaca pada hari pertama 2 halaman, hari kedua 4 halaman, hari ketiga 8 halaman, dan seterusnya, maka buku tersebut akan selesai dibaca pada hari ke ….

S7

Dalam hidupnya, suatu jenis bakteri membelah diri menjadi dua bagian setiap menit. Jika mula-mula terdapat 10 bakteri, maka setelah10 menit jumlah bakteri menjadi ….

S8

Dalam hidupnya, suatu jenis bakteri membelah diri menjadi dua bagian setiap menit. Jika mula-mula terdapat 5 bakteri, maka lama waktu yang diperlukan agar bakteri menjadi 640 ekor adalah ….

S9

Sebuah bola dijatuhkan dari ketinggian 8 meter. Kemudian bola tersebut memantul kembali setinggi 6 meter dan seterusnya. Setiap kali menyentuh lantai, bola tersebut akan memantul setinggi $\frac{3}{4}$ kali ketinggian sebelumnya. Panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke 4 kalinya adalah ... meter.

S10

Sebuah bola dijatuhkan dari ketinggian 25 meter. Setiap kali menyentuh lantai, bola tersebut akan memantul setinggi $\frac{4}{5}$ kali ketinggian sebelumnya. Panjang lintasan yang terbentuk sampai bola menyentuh lantai untuk yang ke 5 kalinya adalah …. meter.

Share this post