Contoh Soal Penerapan Barisan dan Deret Aritmatika dalam Kehidupan Sehari-Hari

Contoh Soal Penerapan Barisan dan Deret Aritmatika dalam Kehidupan Sehari-Hari - Pada topik-topik sebelumnya kita telah belajar mengenai barisan dan deret aritmetika. Tahukah kalian bahwa terdapat banyak masalah dalam kehidupan sehari-hari yang merupakan aplikasi dari barisan dan deret aritmetika? Pada topik ini kita akan membahas mengenai masalah-masalah tersebut. Sebelum membahasnya, ayo segarkan ingatanmu mengenai barisan dan deret aritmetika.

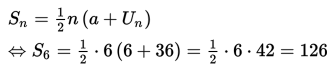
       Barisan aritmetika didefinisikan sebagai barisan bilangan dengan selisih antara dua suku yang berurutan selalu tetap. Selisih antara dua suku yang berurutan pada barisan aritmetika dikenal dengan istilah “beda antarsuku” atau “beda”. Barisan aritmetika memiliki pola sebagai berikut.

a, a + b, a + 2b, a + 3b, ... , a + (n - 1) b

Dengan, 
a = U1 = suku pertama
b = beda antarsuku
a + b = U2 = suku kedua
a + 2b = U3 = suku ketiga
a + 3b = U4 = suku keempat
a + (n - 1)b = Un = suku ke-n

Beda antarsuku pada suatu barisan aritmetika ditentukan menggunakan rumus:

b = Un - Un - 1 atau $b=\frac{U_m-U_n}{m-n}$

Dengan, 
Um = suku ke-m
Un = suku ke-n

Suku ke-n dari suatu barisan aritmetika ditentukan menggunakan rumus:

Un = (n - 1) b

Jika U1 , U2 , U3 , ... , Un adalah suku-suku barisan aritmetika, maka U1 + U2 + U3 + ... + Un disebut deret aritmetika. Jadi, suku-suku dari suatu deret aritmetika berasal dari barisan aritmetika. Jumlah n suku pertama deret aritmetika dapat ditentukan dengan rumus:

$S_n=\frac{1}{2}n(a+U_n)$ atau $S_n=\frac{1}{2}n(2a+(n-1)b)$

       Dalam kehidupan sehari-hari, terdapat beberapa contoh masalah yang dapat diselesaikan dengan menggunakan konsep barisan dan deret aritmetika. Berikut ini adalah beberapa contohnya.

Contoh 1

Fikri memiliki seutas tali rafia yang dipotong menjadi 6 bagian dan membentuk barisan aritmetika. Panjang tali yang terpendek adalah 6 cm dan yang terpanjang 36 cm. Tentukan panjang rafia semula.

Penyelesaian:

banyak potongan tali rafia = n = 6 
panjang tali terpedek = a = 6 cm 
panjang tali terpanjang = U6 = 36

Panjang rafia semula adalah jumlah seluruh panjang potongan tali rafia (S6), sehingga

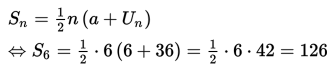
Jadi, panjang tali rafia semula adalah 126 cm.

S1

Pak Ali sedang membuat tembok dari batu bata. Banyak batu bata di tiap lapisan membentuk barisan aritmetika. Jika banyak batu bata di lapisan paling atas adalah 10 buah dan 32 lapis yang sudah dipasang membutuhkan 1.312 batu bata, maka banyak batu bata pada lapisan paling bawah adalah ….

S2

Di sebuah toko bahan bangunan terdapat tumpukan batu bata. Banyak batu bata pada tumpukan paling atas adalah 12 buah dan selalu bertambah 2 buah pada tumpukan di bawahnya. Jika terdapat 40 tumpukan batu bata dari tumpukan bagian atas sampai bawah dan harga setiap batu bata adalah Rp600,00, maka besarnya biaya yang harus dikeluarkan untuk membeli seluruhnya adalah ....

S3

Selvi naik taksi dari Kota A ke Kota B yang berjarak 9 kilometer. Besarnya argo taksi adalah Rp8.000,00 untuk 1 kilometer pertama, kemudian bertambah Rp700,00 tiap 100 meter selanjutnya. Besarnya ongkos taksi yang harus dibayar Selvi adalah ...

S4

Beni menabung sebesar Rp15.000,00 setiap minggu di koperasi sekolah. Setelah menabung selama 4 bulan, Beni mengambil seluruh tabungannya yaitu sebesar Rp399.000,00. Besar tabungan awal Beni adalah ...

S5

Santi memiliki beberapa potong pita yang membentuk barisan aritmetika. Panjang pita-pita tersebut masing-masing adalah 30 cm, 50 cm, 70 cm, … , 170 cm. Panjang pita Santi seluruhnya adalah ….

S6

Arifin memiliki beberapa potongan tali yang panjangnya membentuk barisan aritmetika. Panjang tali yang terpendek adalah 25 cm. Jika selisih panjang masing-masing tali adalah 5 cm dan panjang tali seluruhnya ada 225 cm, maka banyaknya potongan tali yang dimiliki oleh Arifin adalah ….

S7

Seutas kawat dipotong menjadi 5 bagian sehingga membentuk barisan aritmetika. Jika panjang kawat terpendek adalah 1,5 meter dan yang terpanjang 3,5 meter, maka panjang kawat mula-mula adalah ….

S8

Dalam suatu gedung pertemuan terdapat barisan-barisan kursi dengan 8 buah kursi di barisan terdepan, dan banyaknya kursi pada baris-baris berikutnya selalu lebih banyak 5 kursi dibanding baris sebelumnya. Jika terdapat 10 baris kursi, maka banyaknya kursi dalam gedung tersebut adalah ….

S9

Dalam sebuah aula terdapat 136 buah kursi yang disusun dalam beberapa baris. Baris pertama terdiri atas 10 buah kursi, dan baris berikutnya memuat dua kursi lebih banyak dibanding baris sebelumnya. Banyak baris kursi dalam gedung tersebut adalah ….

S10

Dalam sebuah ruangan terdapat beberapa buah bangku yang disusun menjadi beberapa baris. Banyaknya kursi di baris pertama adalah 15 buah, sedangkan di baris ke-4 terdapat 27 buah kursi. Banyaknya kursi di baris ke-6 adalah ….

Share this post