Menghitung Luas bayangan Bangun Datar
Menghitung Luas bayangan Bangun Datar - Pada topik sebelumnya, kalian telah belajar tentang transformasi titik, garis, dan kurva. Kalian tentu mengetahui bahwa dari beberapa titik dan beberapa garis dapat dibuat bidang datar. Nah, kali ini kalian akan belajar tentang cara menentukan luas bayangan dari bangun datar setelah ditransformasi.
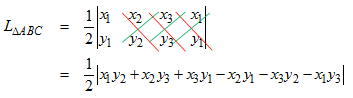
Nah, untuk mempermudah pemahaman kalian tentang bagaimana menentukan luas bayangan bangun datar, mari kita perhatikan contoh berikut.
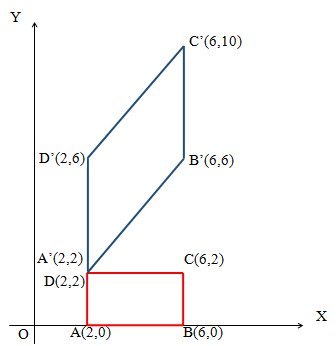
Agar kalian lebih jelas, mari kita perhatikan beberapa contoh berikut.
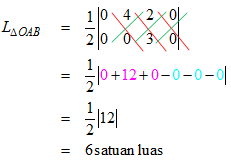
Ayo uji pemahaman kalian dengan mengerjakan sepuluh latihan soal yang ada dalam topik ini.
Sebagaimana kalian ketahui, suatu bangun datar jika ditransformasi akan mengalami perubahan. Adapun perubahan tersebut dapat berupa posisi atau letak, dapat pula bentuk bangunnya, atau juga ukurannya.
Sebelum membahas lebih lanjut tentang luas bayangan bangun ruang, mari kita ingat kembali cara menghitung luas segitiga jika diketahui koordinat ketiga titik sudutnya.
Luas Segitiga Sebarang
Luas segitiga ABC dengan koordinat titik-titik sudut A(x1, y1), B(x2, y2), dan C(x3, y3) dapat ditentukan dengan menggunakan rumus berikut:
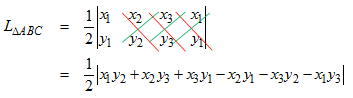
Nah, untuk mempermudah pemahaman kalian tentang bagaimana menentukan luas bayangan bangun datar, mari kita perhatikan contoh berikut.
Contoh 1
Tentukan luas bayangan persegi panjang ABCD dengan koordinat A((2, 0), B(6,0), C(6, 2), dan D(2,2) jika ditransformasikan terhadap matriks berikut:
Penyelesaian:
(1)
Berdasarkan konsep transformasi, diperoleh hasil transformasi sebagai berikut:
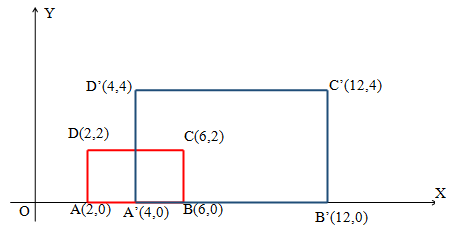
Berdasarkan uraian di atas, dapat kita simpulkan bahwa bayangan titik A, B, C, dan D berturut-turut adalah A’(4, 0), B’(12, 0), C’(12, 4), dan D’(4, 4).

Berdasarkan gambar di atas, tampak bahwa bentuk bayangan hasil transformasi masih berupa persegi panjang.
Luas A’B’C’D’ = A’B’ x A’D’= 8 x 4 = 32 satuan luas.
(2)
Berdasarkan konsep transformasi, diperoleh hasil transformasi sebagai berikut:
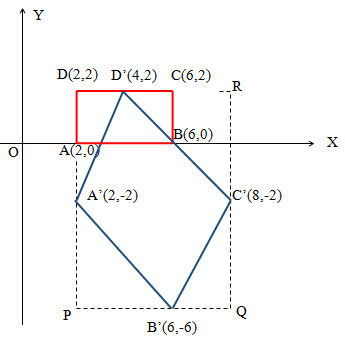
Berdasarkan uraian di atas, dapat kita simpulkan bahwa bayangan titik A, B, C, dan D berturut-turut adalah A’(2, -2), B’(6, -6), C’(8, -2), dan D’(4, 2).

Berdasarkan gambar di atas, tampak bahwa bentuk bayangan hasil transformasi berupa
jajar genjang.
jajar genjang.
Untuk menentukan luas segiempat A’B’C’D’, perhatikan persegi panjang PQRD dengan PQ = 6 cm dan QR = 8 cm.
Luas A’B’C’D’
= Luas PQRD – Luas ΔPB’A’ – Luas ΔB’QC’ – Luas ΔC’RD’ – Luas ΔA’D’D
= (6 x 8) – (½ x PB’ x PA’) – (½ x B’Q x QC’) – (½ x C’R x RD’) – (½ x A’D x DD’)
= 48 – (½ x 4 x 4) – (½ x 2 x 4) – (½ x 4 x 4) – (½ x 4 x 2)
= 48 – 8 – 4 – 8 – 4
= 24 satuan luas
= Luas PQRD – Luas ΔPB’A’ – Luas ΔB’QC’ – Luas ΔC’RD’ – Luas ΔA’D’D
= (6 x 8) – (½ x PB’ x PA’) – (½ x B’Q x QC’) – (½ x C’R x RD’) – (½ x A’D x DD’)
= 48 – (½ x 4 x 4) – (½ x 2 x 4) – (½ x 4 x 4) – (½ x 4 x 2)
= 48 – 8 – 4 – 8 – 4
= 24 satuan luas
(3)
Berdasarkan konsep transformasi, diperoleh hasil transformasi sebagai berikut:
Berdasarkan uraian di atas, dapat kita simpulkan bahwa bayangan titik A, B, C, dan D berturut-turut adalah A’(2, 2), B’(6, 6), C’(6, 10), dan D’(2, 6).
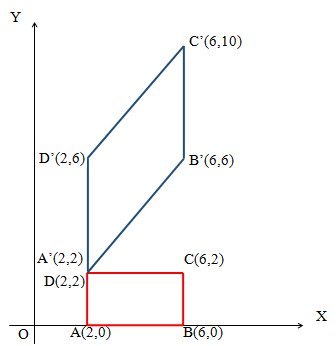
Berdasarkan gambar di atas, tampak bahwa bentuk bayangan hasil transformasi berupa jajar genjang.
Luas Bayangan Bangun Datar
Apa yang dapat kalian simpulkan dari hasil yang diperoleh pada contoh 1?
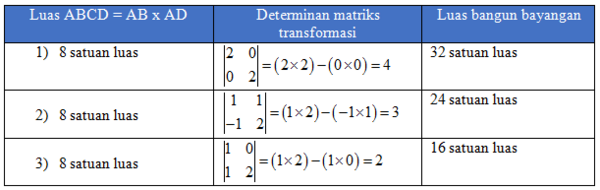
Mari kita perhatikan tabel berikut.

Berdasarkan tabel di atas, tampak bahwa luas bangun bayangan sama dengan determinan matriks transformasi dikalikan dengan luas bangun semula.
Secara umum, jika suatu bangun datar dengan luas L ditransformasikan oleh suatu transformasi yang bersesuaian dengan matriks , maka luas bangun bayangannya adalah .
Agar kalian lebih jelas, mari kita perhatikan beberapa contoh berikut.
Contoh 2
Diketahui segitiga OAB dengan koordinat titik sudutnya adalah O(0, 0), A(4, 0), dan B(2, 3). Jika segitiga OA’B’ adalah bayangan dari segitiga OAB oleh transformasi yang bersesuaian dengan matriks , maka tentukan luas bangun bayangannya.
Penyelesaian:
Dengan menggunakan pendekatan koordinat, luas bangun segitiga OAB adalah
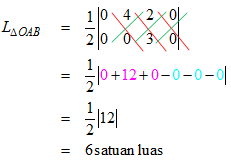
Dengan demikian, luas bayangan dari ∆OAB adalah .
Contoh 3
Diketahui persegi ABCD dengan koordinat titik sudutnya adalah A(–2, 0), B(0, –2), C(2, 0), dan D(0, 2). Titik A’, B’, C’, dan D’ adalah titik hasil transformasi persegi ABCD dengan matriks . Hitunglah luas bayangan persegi tersebut.
Penyelesaian:
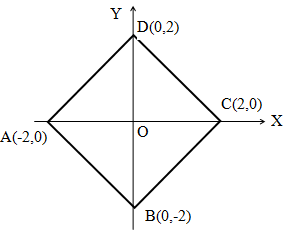
Perhatikan gambar persegi ABCD berikut:

Dari gambar di atas, tampak bahwa panjang AO = BO = 2 satuan panjang.
Dengan demikian, persegi ABCD memiliki ukuran panjang sisi = satuan panjang dan luasnya adalah satuan luas.
Jadi, luas bayangan dari persegi ABCD adalah 8 satuan luas.
Contoh 4
Diketahui segitiga PQR dengan koordinat titik sudut P(-3, 4), Q(1,1), dan R(3, 4). Jika segitiga P’Q’R’ adalah bayangan segitiga PQR oleh transformasi yang bersesuaian dengan matriks , maka tentukan luas P’Q’R’.
Penyelesaian:
Dengan menggunakan pendekatan koordinat, maka luas segitiga PQR adalah
Dengan demikian, luas bangun segitiga PQ’R’ oleh transformasi adalah
Ayo uji pemahaman kalian dengan mengerjakan sepuluh latihan soal yang ada dalam topik ini.
luas bayangan segitiga,
cara mencari luas bayangan persegi panjang,
mencari luas segitiga dengan matriks,
contoh soal dan pembahasan transformasi matriks,
contoh soal dilatasi,
komposisi transformasi geometri,
soal transformasi geometri kelas 12,
contoh soal refleksi,