Contoh Soal Nilai Maksimum dan Minimum Fungsi

Contoh Soal Nilai Maksimum dan Minimum Fungsi - Coba perhatikan kembali grafik fungsi f (x) = 4x – x2 yang telah disajikan pada topik fungsi naik dan fungsi turun.

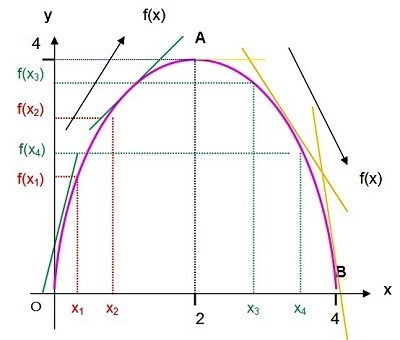
Dalam topik itu telah kita bahas mengenai definisi fungsi naik dan fungsi turun, yaitu sebagai berikut.

Fungsi Naik dan Fungsi Turun

Misalkan fungsi f didefinisikan pada Df.

1. Fungsi f dikatakan fungsi naik pada Df jika dan hanya jika untuk setiap x1, x2 ∈ Df , dengan x1 < x2 menyebabkan f(x1) < f(x2).
2. Fungsi f dikatakan fungsi turun pada Df jika dan hanya jika untuk setiap x1, x2 ∈ Df , dengan x1 < x2 menyebabkan f(x1) > f(x2).

Dengan menggunakan konsep turunan, kita juga dapat menentukan fungsi naik dan fungsi turun menggunakan Teorema Kemonotonan berikut.

Teorema Kemonotonan

Misalkan fungsi f didefinisikan dan mempunyai turunan pada Df.

1. Jika f ‘(x) > 0 untuk x ∈ Df , maka fungsi f dikatakan fungsi naik pada Df.
2. Jika f ‘(x) < 0 untuk x ∈ Df , maka fungsi f dikatakan fungsi turun pada Df.
3. Jika f ‘(x) = 0 untuk x ∈ Df , maka fungsi f dikatakan fungsi stasioner pada Df.

Ayo, perhatikan kembali grafik fungsi f(x) = 4x – x2 .

Pada titik A, kamu mendapatkan nilai fungsi terbesar dari semua nilai fungsi untuk setiap x ∈ Df. Nilai terbesar dari fungsi ini disebut nilai maksimum fungsi. Sebaliknya, nilai terkecil dari fungsi disebut nilai minimum fungsi.

Misalkan fungsi f kontinu dan mempunyai turunan pada interval tertutup Df dan c ∈ Df .

1. Jika f(c) ≥ f(x) untuk setiap x ∈ Df , maka f(c) disebut nilai fungsi maksimum fungsi f(x).
2. Jika f(c) ≤ f(x) untuk setiap x ∈ Df , maka f(c) disebut nilai fungsi minimum fungsi f(x).

        Dimanakah kamu mungkin menemukan nilai maksimum dan minimum fungsi ini? Nilai-nilai tersebut dapat kamu temukan pada titik kritis fungsi dan pada titik-titik ujung interval. Titik kritis adalah titik stasioner dan titik yang turunannya tidak ada.

        Jika kamu mendapatkan titik kritis fungsi, yaitu bila f ‘(c) = 0 atau f ‘(c) tidak ada untuk c ∈ Df maka dengan melakukan uji turunan kedua, f “(c), kamu dapat mengetahui apakah f(c) merupakan nilai maksimum atau minimum.

Nilai Minimum dan Maksimum Fungsi

Misalkan fungsi f kontinu dan mempunyai turunan pertama dan turunan kedua pada interval Df yang memuat x = c dan f '(c) = 0 atau f '(c) tidak ada.

1. Jika f "(c) < 0, maka f(c) adalah nilai maksimum fungsi f.
2. Jika f "(c) > 0, maka f(c) adalah nilai minimum fungsi f.
3. Jika f "(c) = 0, maka nilai stasioner f(c) belum dapat ditentukan. Dalam kasus f "(c) = 0, penentuan jenis-jenis nilai stasioner kembali menggunakan uji turunan pertama.

SOAL 1

Titik kritis dari fungsi f(x) = 2 + x−−√3$\sqrt[3]{x}$ adalah ….

SOAL 2

Titik balik maksimum dari grafik f(x) = x3 – 12x + 3 adalah ….

SOAL 3

Nilai maksimum fungsi g(x) = x4 - 12$\frac{1}{2}$ x pada interval 0 ≤ x ≤ 2 adalah ….

SOAL 4

Titik balik maksimum dari grafik fungsi f(t) = (t2 + 1)(t3 – 1) adalah ….

SOAL 5

Fungsi f(x) = |x| mencapai minimum pada titik ….

SOAL 6

Jika x = sin t maka f(x) = x2 – 4x + 3 akan mencapai nilai minimum untuk x = ….

SOAL 7

Absis titik balik grafik fungsi f(x) = px² + (p - 3)x + 2 adalah p. Nilai p adalah ....

SOAL 8

Fungsi f(x) = x3 – kx2 – 9x + 7 mencapai maksimum pada x = -1 untuk nilai k = ….

SOAL 9

Jika fungsi f(x) = x(12 – 2x)2 mempunyai nilai maksimum p dan nilai minimum q, maka p – q = ….

SOAL 10

Nilai maksimum dan minimum fungsi f(x) = (sin x + cos x)2 , 0⁰ ≤ x ≤ 180⁰ berturut-turut adalah ….

Share this post