Contoh Soal Titik Stasioner Suatu Fungsi Beserta Jenis Ekstrimnya
Contoh Soal Titik Stasioner Suatu Fungsi Beserta Jenis Ekstrimnya - Setelah mempelajari materi tentang fungsi naik dan fungsi turun, selanjutnya kamu akan mempelajari titik stasioner suatu fungsi dengan menerapkan turunan fungsi.
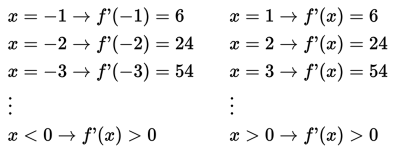

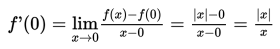
Perhatikan grafik di bawah ini.

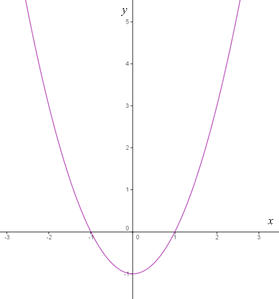
Grafik di atas menggambarkan sebuah fungsi kuadrat y = f (x) = x2 – 1 dan mempunyai nilai minimum pada x = 0 karena f (0) = 0 – 1 = -1. Sekarang, coba kamu perhatikan dimana grafik tersebut naik dan turun. Turunan fungsi tersebut atau f ‘ (x) adalah f ‘ (x) = 2x. Dari grafik diperoleh:
untuk x = 0, maka f ‘ (0) = 0
untuk x < 0, maka f ‘ (x) < 0
untuk x > 0, maka f ‘ (x) > 0
untuk x < 0, maka f ‘ (x) < 0
untuk x > 0, maka f ‘ (x) > 0
Mengapa untuk x < 0 nilai f ‘ (x) < 0, sedangkan untuk x > 0 nilai f ‘ (x) > 0? Mari simak jawabannya sebagai berikut.
Untuk x < 0
Misal:
x = -1 → f ‘ (-1) = -2
x = -2 → f ‘ (-2) = -4
x = -3 → f ‘ (-3) = -6
⁞
x < 0 → f ‘ (x) < 0
Misal:
x = -1 → f ‘ (-1) = -2
x = -2 → f ‘ (-2) = -4
x = -3 → f ‘ (-3) = -6
⁞
x < 0 → f ‘ (x) < 0
Untuk x > 0
Misal:
x = 1 → f ‘ (1) = 2
x = 2 → f ‘ (2) = 4
x = 3 → f ‘ (3) = 6
⁞
x > 0 → f ‘ (x) > 0
Misal:
x = 1 → f ‘ (1) = 2
x = 2 → f ‘ (2) = 4
x = 3 → f ‘ (3) = 6
⁞
x > 0 → f ‘ (x) > 0
Ini berarti fungsi f turun di titik x < 0 dan naik di titik x > 0. Bagaimana dengan titik x = 0, apakah fungsi f naik ataukah turun di titik tersebut? Perhatikan kembali grafik di atas. Grafik tersebut menunjukkan bahwa di titik x = 0 yang merupakan titik minimum dari fungsi, fungsi f tidak naik maupun turun. Titik seperti ini dinamakan titik stasioner.
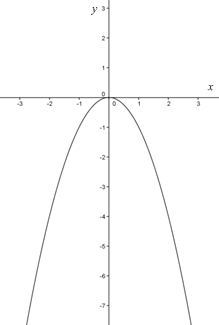
Perhatikan grafik di bawah ini. Manakah yang merupakan titik maksimum fungsi?

Titik x = 0 merupakan titik maksimum fungsi. Dimanakah fungsi tersebut naik dan turun? Grafik di atas didefinisikan sebagai f (x) = - x2 . Turunan fungsi tersebut adalah f ‘ (x) = - 2x. Dari grafik diperoleh:
untuk x = 0, maka f ‘ (0) = 0
untuk x < 0, maka f ‘ (x) > 0
untuk x > 0, maka f ‘ (x)< 0
untuk x < 0, maka f ‘ (x) > 0
untuk x > 0, maka f ‘ (x)< 0
Mengapa untuk x < 0 nilai f ‘ (x) > 0, sedangkan untuk x > 0 nilai f ‘ (x) < 0? Mari simak jawabannya sebagai berikut.
Untuk x < 0
Misal:
x = -1 → f ‘ (-1) = 2
x = -2 → f ‘ (-2) = 4
x = -3 → f ‘ (-3) = 6
⁞
x < 0 → f ‘ (x) > 0
Misal:
x = -1 → f ‘ (-1) = 2
x = -2 → f ‘ (-2) = 4
x = -3 → f ‘ (-3) = 6
⁞
x < 0 → f ‘ (x) > 0
Untuk x > 0
Misal:
x = 1 → f ‘ (1) = -2
x = 2 → f ‘ (2) = -4
x = 3 → f ‘ (3) = -6
⁞
x > 0 → f ‘ (x) < 0.
Ini berarti, fungsi naik pada x < 0 dan turun pada x > 0. Pada titik x = 0 fungsi tidak naik dan tidak turun atau f ‘ (0) = 0, sehingga titik x = 0 merupakan titik stasioner dari fungsi tersebut. Dengan demikian, y = f (x) dikatakan stasioner pada x = a, jika f ‘ (a) = 0 dan diferensiabel di titik tersebut, serta nilai f (a) dinamakan nilai stasioner.
Misal:
x = 1 → f ‘ (1) = -2
x = 2 → f ‘ (2) = -4
x = 3 → f ‘ (3) = -6
⁞
x > 0 → f ‘ (x) < 0.
Ini berarti, fungsi naik pada x < 0 dan turun pada x > 0. Pada titik x = 0 fungsi tidak naik dan tidak turun atau f ‘ (0) = 0, sehingga titik x = 0 merupakan titik stasioner dari fungsi tersebut. Dengan demikian, y = f (x) dikatakan stasioner pada x = a, jika f ‘ (a) = 0 dan diferensiabel di titik tersebut, serta nilai f (a) dinamakan nilai stasioner.
Titik stasioner (f ‘ (x) = 0) adalah titik dimana fungsi tidak naik ataupun turun sehingga gradiennya adalah 0 atau garis singgungnya merupakan sebuah garis mendatar. Bagaimana dengan titik stasioner pada fungsi lain (bukan fungsi kuadrat) seperti pada fungsi kubik dan fungsi mutlak? Perhatikan penjelasan berikut ini.
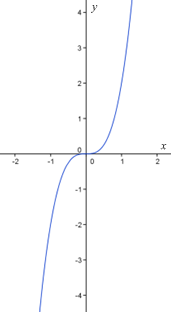
• Fungsi f (x) = 2x3 digambarkan pada grafik di bawah ini.

Mari kita periksa keadaan saat fungsi tersebut naik, turun dan titik stasionernya.
f (x) = 2 x3 → f ‘ (x) = 6x2
f (x) = 2 x3 → f ‘ (x) = 6x2
Untuk:
x = 0 → f (0) = 0 dan f ‘ (0) = 0
x = 0 → f (0) = 0 dan f ‘ (0) = 0
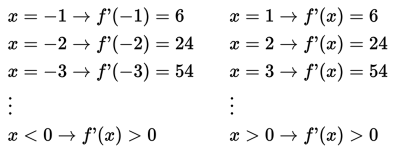
Ini berarti, fungsi naik pada x < 0 atau x > 0 dan titik x = 0 merupakan titik stasioner merupakan titik stasioner namun bukan merupakan titik ekstrem (maksimum atau minimum) fungsi tersebut.
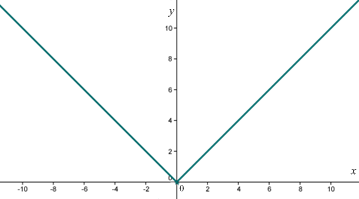
• Fungsi y = f (x) = |x| digambarkan pada grafik di bawah ini.


Ini berarti, f ‘ (x) = 1 untuk x > 0 dan f ‘ (x) = -1 untuk x < 0.
Untuk x = 0
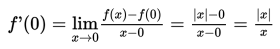
Berdasarkan pembahasan sebelumnya, maka diketahui bahwa limit fungsi tersebut tidak ada sehingga f ‘ (0) tidak terdiferensialkan. Jadi, dapat disimpulkan bahwa untuk f (x) = |x|, f (x) naik pada x > 0 dan f (x) turun pada x < 0, dan titik x = 0 bukan merupakan titik stasioner.
SOAL 1
Nilai absis koordinat titik stasioner yang tepat untuk kurva y = f (x) = 2x2 + 3 adalah …
SOAL 2
Absis koordinat titik stasioner pada kurva y = (x - 2)2 + 3 adalah ….
SOAL 4
Diketahui sebuah fungsi f (x) = x2 + px + 5 memiliki titik stasioner x = -2, maka nilai p adalah ….
SOAL 5
Diketahui sebuah fungsi f (x) = 2x2 + (p + 2)x memiliki titik stasioner x = 0, maka titik stasioner fungsi f (x) = px2 adalah ….
SOAL 6
Jenis titik balik yang dipenuhi oleh fungsi f (x) = x (x2 - 12) dan nilai titik baliknya adalah ….
SOAL 7
Titik balik maksimum fungsi f (x) = x3 + 6x2 – 15x + 9 adalah ….
SOAL 8
Absis koordinat titik balik minimum suatu fungsi f (x) = (x2 -16)2 adalah a + 12, maka nilai f (a) adalah ….
SOAL 9
Diketahui koordinat titik balik maksimum fungsi adalah (a, b). Jika f (x) = - x2 + (b + 1)x dan (a + b)2= 1, maka koordinat titik balik maksimum fungsi tersebut adalah …
SOAL 10
Diketahui dengan . Jika merupakan nilai absis titik stasioner fungsi tersebut, maka fungsi itu adalah ….
