Transformasi Garis dan Kurva Menggunakan Matriks Tunggal

Transformasi Garis dan Kurva Menggunakan Matriks Tunggal - Bentuk matriks dapat digunakan dalam transformasi. Adapun transformasi merupakan fungsi yang memetakan titik semula ke bayangan titik tersebut.

Pada topik sebelumnya, kalian telah belajar tentang transformasi titik dengan menggunakan matriks tunggal. Nah, pada topik ini kalian akan belajar tentang cara menentukan bayangan garis atau kurva dengan menggunakan matriks transformasi tunggal.

Kalian pasti tidak akan merasa kesukaran dalam mempelajari materi ini karena pada dasarnya transformasi garis maupun kurva dengan menggunakan matriks tunggal caranya sama dengan melakukan transformasi titik.

Apakah kalian tahu sebabnya?

Ya, hal ini dikarenakan garis maupun kurva adalah himpunan titik-titik yang memenuhi syarat tertentu.

Untuk mempermudah kalian dalam mempelajari topik ini, mari kita cermati beberapa contoh soal berikut.

Contoh 1

Tentukan bayangan garis 2x + 3y = 6 oleh suatu matriks (46 ) $\left(\begin{array}{c}4\\ 6\end{array}\right)$.

Penyelesaian:

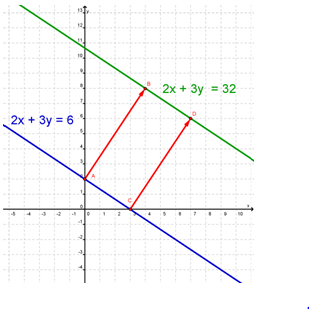
Agar kalian dengan mudah memahami masalah ini, mari kita perhatikan gambar berikut ini:

Pada gambar di atas, dapat kalian lihat bahwa titik A dipindahkan ke titik B, titik C dipindahkan ke titik D, dan setiap titik (x, y) pada garis 2x + 3y = 6 dipindahkan oleh suatu transformasi berupa matriks (46 ) $\left(\begin{array}{c}4\\ 6\end{array}\right)$ sehingga diperoleh titik yang baru, yaitu titik (x', y') yang merupakan bayangan hasil transformasi oleh matriks tersebut.

Lebih lanjut, matriks (46 ) $\left(\begin{array}{c}4\\ 6\end{array}\right)$ memetakan setiap titik (x, y) ke (x', y') dengan cara memindahkan titik (x, y) ke kanan sejauh 4 satuan dan ke atas sejauh 6 satuan. Adapun bayangan yang dihasilkan oleh transformasi tersebut adalah 2x + 3y = 32.

Konsep Dasar I

Jika kalian hendak mencari persamaan garis hasil transformasi tanpa menggunakan gambar, maka kalian perlu menggunakan hubungan berikut: (x′y′ )=(x+ay+b ) $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}x+a\\ y+b\end{array}\right)$.

Perlu kalian ketahui, titik (x, y) adalah titik yang akan ditransformasikan terhadap matriks (ab ) $\left(\begin{array}{c}a\\ b\end{array}\right)$, sedangkan (x', y') adalah titik hasil transformasi.

Mari kita perhatikan kembali contoh 1.

Dalam contoh 1, matriks transformasi yang digunakan adalah (46 ) $\left(\begin{array}{c}4\\ 6\end{array}\right)$, sehingga diperoleh hubungan sebagai berikut:

(x′y′ )=(x+4y+6 )⇔(xy )=(x′−4y′−6 ) $\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)=\left(\begin{array}{c}x+4\\ y+6\end{array}\right)\iff \left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}{x}^{\prime }-4\\ y^{\prime }-6\end{array}\right)$

Selanjutnya jika kita subtitusikan x = x' - 4 dan y = y' - 6 ke dalam persamaan garis 2x + 3y = 6, maka diperoleh persamaan garis yang baru, yaitu:

2(x′−4)+3(y′−6)=6⇔2x′−8+3y′−18=6⇔2x′+3y′=32  $\begin{array}{rl}& 2(x^{\prime }-4)+3(y^{\prime }-6)=6\\ & \iff 2x^{\prime }-8+3y^{\prime }-18=6\\ & \iff 2x^{\prime }+3y^{\prime }=32\end{array}$

Dengan demikian, bayangan garis 2x + 3y = 6 oleh transformasi matriks (46 ) $\left(\begin{array}{c}4\\ 6\end{array}\right)$ adalah 2x + 3y = 32.

Mudah bukan?

Contoh 2

Tentukan bayangan parabola y = x2 - 4x + 4 oleh matriks (−12 ) $\left(\begin{array}{c}-1\\ 2\end{array}\right)$.

Penyelesaian:

Untuk menyelesaikan soal ini, kita gunakan hubungan sebagai berikut:

(x′y′ )⇔(x′y′ )⇔(xy )===(x+ay+b )(x+(−1)y+2 )(x′+1y′−2 )  $\begin{array}{ccc}\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{c}x+a\\ y+b\end{array}\right)\\ \iff \left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right)& =& \left(\begin{array}{c}x+(-1)\\ y+2\end{array}\right)\\ \iff \left(\begin{array}{c}x\\ y\end{array}\right)& =& \left(\begin{array}{c}{x}^{\prime }+1\\ y^{\prime }-2\end{array}\right)\end{array}$

Berdasarkan uraian di atas, tampak bahwa x = x' + 4 dan y = y' - 2.

Selanjutnya jika kita subtitusikan hasil tersebut ke dalam persamaan parabola y = x2 - 4x + 4, maka diperoleh hasil sebagai berikut:

y=x2−4x+4 $y=x^2-4x+4$
⇔y′−2=(x′+1)2−4(x′+1)+4 $\iff y^{\prime }-2={\left(x^{\prime }+1\right)}^2-4\left(x^{\prime }+1\right)+4$
⇔y′−2=(x′)2+2x′+1−4x′−4+4 $\iff y^{\prime }-2={\left(x^{\prime }\right)}^2+2x^{\prime }+1-4x^{\prime }-4+4$
⇔y′=(x′)2−2x′+3 $\iff y^{\prime }={\left(x^{\prime }\right)}^2-2x^{\prime }+3$

Dengan demikian, bayangan parabola y = x2 - 4x + 4 oleh matriks (−12 ) $\left(\begin{array}{c}-1\\ 2\end{array}\right)$ adalah y = x2- 2x + 3.

Konsep Dasar II

Dalam menyelesaikan masalah transformasi dengan menggunakan matriks, kita akan sering menemui persamaan matriks berbentuk A=BX $A=BX$ dan terkadang kita perlu menentukan matriks X tersebut.

Nah, untuk menentukan matriks X, kita gunakan hubungan berikut: A=BX⇔X=B−1A $A=BX\iff X=B^{-1}A$.

Perlu kalian ingat, jika matriks B=(acbd ) $B=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$, maka B-1=1ad−bc(d−c−ba ) $=\frac{1}{ad-bc}\left(\begin{array}{cc}d& -b\\ -c& a\end{array}\right)$.

Agar kalian lebih paham mengenai konsep dasar di atas, mari kita perhatikan beberapa contoh berikut.

Tentukan bayangan garis 2x - 3y = 12 oleh matriks transformasi (0−110 ) $\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$.

Penyelesaian:

Jika kita gunakan konsep A=BX⇔X=B−1A $A=BX\iff X=B^{-1}A$, maka diperoleh hasil sebagai berikut:

Selanjutnya, jika kita subtitusikan x = -y' dan y = x' ke dalam persamaan garis 2x - 3y = 12 , maka diperoleh hasil sebagai berikut:

2x−3y⇔2(−y′)−3(x′)⇔−2y′−3x′⇔3x′+2y′====121212−12  $\begin{array}{lll}2x-3y& =& 12\\ \iff 2(-y^{\prime })-3(x^{\prime })& =& 12\\ \iff -2y^{\prime }-3x^{\prime }& =& 12\\ \iff 3x^{\prime }+2y^{\prime }& =& -12\end{array}$

Dengan demikian, bayangan garis 2x - 3y = 12 oleh matriks transformasi (0−110 ) $\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right)$adalah 3x + 2y = -12.

Nah, kalian telah belajar mengenai transformasi garis dan kurva dengan menggunakan matriks tunggal. Ayo kerjakan latihan soal yang ada dalam topik ini untuk menguji pemahaman kalian.

komposisi transformasi dengan matriks,

contoh soal dan pembahasan transformasi matriks,

contoh soal komposisi transformasi dan penyelesaiannya,

pencerminan terhadap garis y=mx+c,

pencerminan terhadap garis y=2x,

transformasi rotasi,

matriks transformasi geometri,

komposisi transformasi geometri,

Share this post