Contoh Soal Memahami Persamaan Garis Sederhana
Contoh Soal Memahami Persamaan Garis Sederhana - Pada topik sebelumnya, kalian telah berlajar bagaimana menentukan letak suatu titik terhadap garis yang dinyatakan dalam koordinat Cartesius. Masih ingatkah kalian tentang topik tersebut?
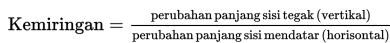
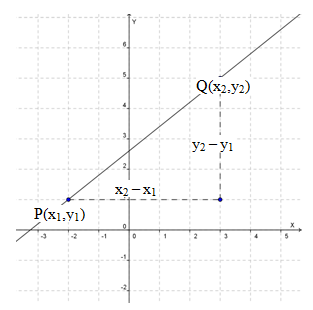
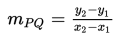
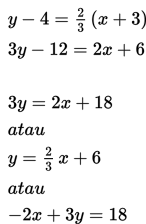
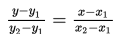
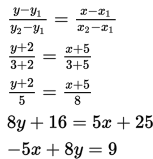
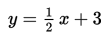
Jika titik-titik yang kalian miliki tersebut dihubungkan dengan garis lurus, maka kalian dapat menemukan banyak sekali garis-garis lurus dalam sistem koordinat.
Nah, kali ini kalian akan belajar tentang persamaan garis sederhana.
Nah, kali ini kalian akan belajar tentang persamaan garis sederhana.
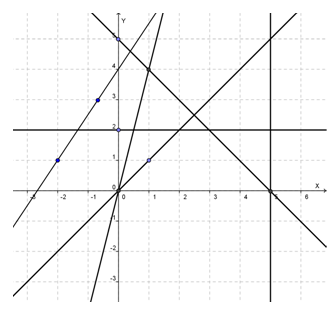
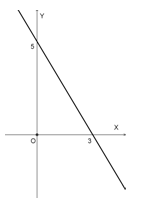
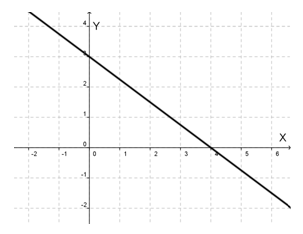
Sebagaimana yang kalian ingat, pada koordinat Cartesius kita bisa menentukan koordinat titik-titik yang diketahui. Selain menggambar titik, di dalam koordinat Cartesius kita dapat menggambarkan garis-garis. Coba perhatikan Gambar 1 berikut ini

Nampak, bahwa banyak sekali garis yang dapat kita gambar pada koordinat Cartesius.
Pertanyaanya, bagaimana cara menggambar garis tersebut jika diketahui persamaannya? Atau bagaimana cara menentukan persamaannya?
Pertanyaanya, bagaimana cara menggambar garis tersebut jika diketahui persamaannya? Atau bagaimana cara menentukan persamaannya?
Mari kita belajar menggambar garis lebih dahulu jika diketahui persamaannya. Perhatikan gambar garis-garis pada Gambar 1, dalam setiap garis ada banyak sekali titik-titik yang dilaluinya. Untuk menggambar garis kita butuh minimal dua titik dan kita hubungkan.
Contoh:
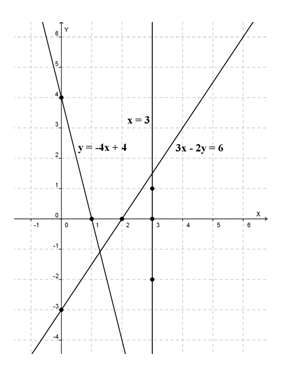
Gambarlah garis-garis y = -4x + 4, x = 3, dan 3x – 2y = 6 dalam satu koordinat.
Penyelesaian:
Untuk menggambar, kita ambil sebarang titik yang terletak pada garis tersebut, caranya
1) Untuk persamaan y = -4x + 4
jika x = 0 maka y = -4(0) + 4 = 4, kita peroleh titik (0,4)
jika y = 0 maka 0 = -4x + 4 => 4x = 4 => x = 1, kita peroleh titik (1,0)
jika x = 0 maka y = -4(0) + 4 = 4, kita peroleh titik (0,4)
jika y = 0 maka 0 = -4x + 4 => 4x = 4 => x = 1, kita peroleh titik (1,0)
2) Untuk persamaan x = 3
jika y = 0 maka x = 3, kita peroleh titik (3,0)
jika y = 1 maka x = 3, kita peroleh titik (3,1)
jika y = -2 maka x = 3, kita peroleh titik (3,-2)
jika y = 0 maka x = 3, kita peroleh titik (3,0)
jika y = 1 maka x = 3, kita peroleh titik (3,1)
jika y = -2 maka x = 3, kita peroleh titik (3,-2)
3) Untuk persamaan 3x – 2y = 6
jika x = 0 maka 3(0) – 2y = 6 => y = -3, kita peroleh titik (0,-3)
jika y = 0 maka 3x – 2(0) = 6 => x = 2, kita peroleh titik
jika x = 0 maka 3(0) – 2y = 6 => y = -3, kita peroleh titik (0,-3)
jika y = 0 maka 3x – 2(0) = 6 => x = 2, kita peroleh titik
Kita letakkan titik-titik tersebut dalam koordinat Cartesius dan dihubungkan, sehingga diperoleh gambar garis berikut

Setelah paham bagaimana menggambar garis, berikutnya kita akan menentukan persamaan garis. Sebelum belajar tentang persamaan garis, ada baiknya kalian belajar tentang kemiringan garis atau yang sering disebut gradien.
Kemiringan garis atau gradien adalah
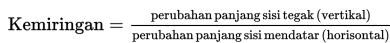
Perhatikan gambar berikut
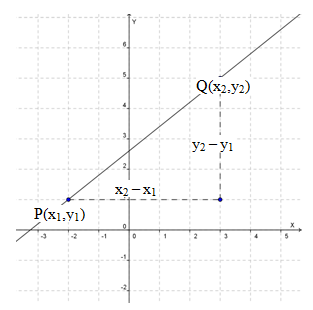
Maka kemiringan garis PQ, ditulis:
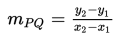
Selanjutnya kita pelajari cara menentukan persamaan garis. Ada beberapa kemungkinan dalam menentukan persamaan garis,yaitu:
1) Jika diketahui kemiringan garis dan titik potong dengan sumbu y, rumusnya adalah
y = mx + c
dengan m adalah gradien garis dan c adalah ordinat titik potong dengan sumbu y
y = mx + c
dengan m adalah gradien garis dan c adalah ordinat titik potong dengan sumbu y
Contoh:
Tentukan persamaan garis yang memiliki kemiringan (gradien) 3 dan memotong sumbu y di titik (0,-8)
Penyelesaian:
Persamaan umumnya adalah y = mx + c
Diketahui m = 3 dan c = -8 jadi persamaan garisnya adalah y = 3x - 8
Diketahui m = 3 dan c = -8 jadi persamaan garisnya adalah y = 3x - 8
2) Jika diketahui suatu garis melalui titik (x1,y1) dan diketahui kemiringan garis (gradien) m maka persamaan garis ditentukan dengan rumus:
y – y1 = m(x – x1)
y – y1 = m(x – x1)
Contoh:
Tentukan persamaan garis yang memiliki kemiringan (gradien) 2/3 dan melalui titik (-3,4)
Penyelesaian:
Persamaan umumnya adalah y – y1 = m(x – x1)
Diketahui m = 2/3danmelalui titik (-3,4) jadi persamaan garisnya adalah
Diketahui m = 2/3danmelalui titik (-3,4) jadi persamaan garisnya adalah
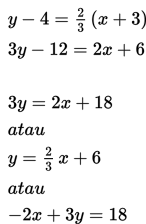
3) Jika diketahui suatu garis melalui titik (x1,y1) dan (x2,y2) maka persamaan garis ditentukan dengan rumus:
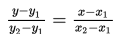
Contoh:
Tentukan persamaan garis yang melalui titik (-5,-2) dan (3,3)
Penyelesaian:
Diketahui garis yang melalui titik (-5,-2) dan (3,3) jadi persamaan garisnya adalah
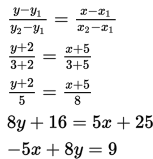
S1
Titik berikut yang terletak pada garis 5x – 3y = 15 adalah ….
S2
Titik (8,-5) dilalui oleh garis ….
S3
Gambar berikut yang merupakan grafik dari persamaan garis
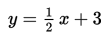
adalah ….
S4
Perhatikan gambar berikut
Persamaan garis yang sesuai dengan grafik tersebut adalah ….
Persamaan garis yang sesuai dengan grafik tersebut adalah ….

S5
Grafik dari persamaan garis 3x – 4y = 6 adalah ….
S6
Diketahui persamaan garis y = -3x + 2, kemiringan garis tersebut adalah ….
S7
Diketahui sebuah garis dengan grafik sebagai berikut.

Kemiringan garis tersebut adalah ….
S8
Sebuah garis diketahui memiliki kemiringan – ½ dan melalui titik (0,5). Persamaan garis tersebut adalah ….
S9
Suatu garis memiliki gradien 2 dan melalui titik (-2,-2). Persamaan garis tersebut adalah ….
S10
Persamaan garis yang melalui titik (-8,7) dan (7,-8) adalah …
