Contoh Soal Jarak Antara Dua Titik
Contoh Soal Jarak Antara Dua Titik - Pada topik sebelumnya, kalian telah belajar mengenai sistem koordinat kartesius. Tentu kalian masih ingat dengan materi tersebut bukan?
Tahukah kalian bagaimana cara menghitung jarak antara dua titik pada bidang kartesius?
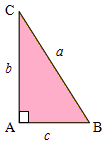
Nah, untuk menentukan jarak antara dua titik, ada dua langkah yang perlu kalian ikuti.
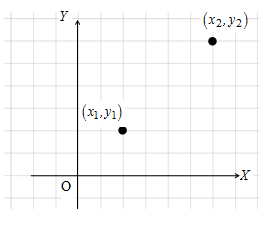
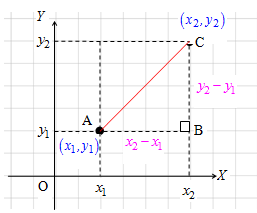
Nah, dari langkah kedua dapat kita simpulkan bahwa jarak antara titik dan adalah .
Apakah kalian sudah paham dengan penjelasan di atas?
Penyelesaian:
Langkah kedua: Menghitung Jarak
Berdasarkan uraian di atas, dapat disimpulkan bahwa jarak antara titik dan adalah 10 satuan.
Dengan menggunakan sistem koordinat kartesius, kalian dapat mendiskripsikan letak sebuah titik. Nah, pada topik kali ini, kalian akan belajar tentang jarak antara dua titik.
Tahukah kalian bagaimana cara menghitung jarak antara dua titik pada bidang kartesius?
Konsep jarak antara dua titik pada bidang kartesius sangat erat kaitannya dengan teorema Pythagoras.
Jika siku-siku di titik , , , dan , maka berdasarkan teorema Pythagoras, .
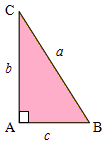
Nah, untuk menentukan jarak antara dua titik, ada dua langkah yang perlu kalian ikuti.
Langkah Pertama:
Misalkan koordinat kedua titik adalah dan .
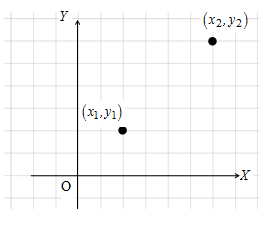
Langkah Kedua:
Buatlah garis lurus yang menghubungkan kedua titik tersebut, kemudian buatlah persegipanjang dimana garis yang menghubungkan kedua titik tersebut merupakan diagonalnya.
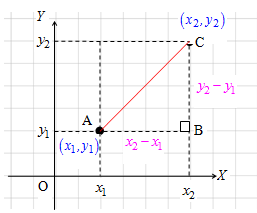
Oleh karena siku-siku di titik , maka berdasarkan teorema Pythagoras, kita peroleh hasil sebagai berikut:
Nah, dari langkah kedua dapat kita simpulkan bahwa jarak antara titik dan adalah .
Apakah kalian sudah paham dengan penjelasan di atas?
Yuk kita cermati beberapa contoh soal berikut agar kalian semakin paham.
Contoh 1
Diberikan titik dan . Berapakah jarak antara titik dan ?
Penyelesaian:
Langkah pertama: Menentukan dan
Misal:
Langkah kedua: Menghitung Jarak
Berdasarkan uraian di atas, dapat disimpulkan bahwa jarak antara titik dan adalah 10 satuan.
S1
Diketahui koordinat titik adalah dan koordinat titik adalah . Jarak antara titik dan adalah ….
S2
Diketahui titik dan . Jarak antara titik dan adalah … satuan.
S3
Diketahui titik dan . Jarak antara kedua titik tersebut adalah … satuan.
S4
Diketahui jarak antara titik dan adalah 17 satuan. Jika titik dan titik , maka nilai yang mungkin adalah ….
S5
Diketahui titik dan titik . Jika jarak antara titik dan adalah 20 satuan, maka salah satu nilai yang mungkin adalah ….
S6
Diketahui titik dan titik . Jarak antara titik dan adalah … satuan.
S7
Diketahui titik dan titik . Jarak antara titik dan adalah … satuan.
S8
Diketahui titik dan titik . Jika jarak antara titik dan adalah satuan, maka nilai yang memenuhi adalah dan . Nilai adalah .…
S9
Diketahui koordinat titik pojok segiempat adalah , , , dan . Panjang sisi terpendek dari segiempat tersebut adalah ….
S10
Diketahui titik , , , dan . Jika jarak antara titik dan lebih pendek dari jarak antara titik dan , maka batasan nilai yang memenuhi adalah ….
