Contoh Soal Konsep Jarak pada Bangun Datar
Contoh Soal Konsep Jarak pada Bangun Datar - Pada topik sebelumnya kalian telah belajar tentang jarak antara dua titik pada bidang kartesius.
Nah, konsep jarak antara dua titik ini juga dapat kalian gunakan untuk menentukan luas dan keliling bangun datar.
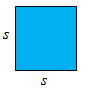
✎ Persegi
✎ Persegipanjang
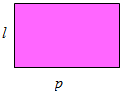
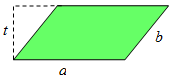
✎ Jajargenjang
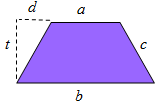
✎ Trapesium
✎ Belah Ketupat
✎ Layang-layang
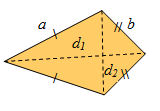
Apakah kalian tahu bagaimana cara menentukan luas dan keliling bangun datar dengan menggunakan konsep jarak antara dua titik?
Penyelesaian:
Jika kita hubungkan titik , dan pada koordinat kartesius, maka kita peroleh sketsa sebagai berikut:
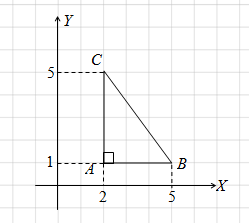
Apakah kalian masih ingat?
Sekedar mengingatkan, jarak antara titik dan dapat dihitung dengan menggunakan kotak satuan pada koordinat kartesius. Namun jika hal tersebut terlalu sulit untuk dilakukan, maka jarak antara kedua titik tersebut dapat dihitung dengan menggunakan rumus: .
Nah, konsep jarak antara dua titik ini juga dapat kalian gunakan untuk menentukan luas dan keliling bangun datar.
Yuk kita ingat kembali rumus luas dan keliling bangun datar.
✎ Persegi

Seperti yang telah kalian ketahui, jika panjang sisi persegi adalah , maka luas persegi tersebut adalah , sedangkan kelilingnya adalah .
✎ Persegipanjang
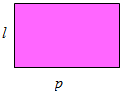
Luas dan keliling sebuah persegipanjang dengan panjang dan lebar berturut-turut adalah dan .
✎ Jajargenjang

Berdasarkan gambar di atas,
- luas jajargenjang =
- keliling jajargenjang =
✎ Trapesium

Oleh karena panjang dua sisi yang sejajar adalah dan , serta tinggi trapesium adalah , maka luas trapesium pada gambar di atas adalah , sedangkan kelilingnya adalah .
✎ Belah Ketupat

Berdasarkan gambar di atas, keliling belah ketupat adalah , sedangkan luasnya adalah .
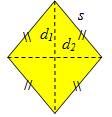
✎ Layang-layang
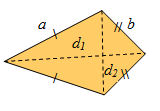
Berdasarkan gambar di atas,
- keliling layang-layang =
- luas layang-layang =
Apakah kalian tahu bagaimana cara menentukan luas dan keliling bangun datar dengan menggunakan konsep jarak antara dua titik?
Yuk kita temukan jawabannya dengan mencermati beberapa contoh soal berikut.
Contoh 1
Diketahui dengan titik , dan . Berapakah luas ?
Penyelesaian:
Jika kita hubungkan titik , dan pada koordinat kartesius, maka kita peroleh sketsa sebagai berikut:
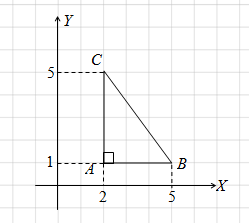
Pada sketsa di atas, tampak bahwa siku-siku di titik , dengan panjang sisi dan berturut-turut adalah satuan dan satuan.
Dengan demikian, luas adalah satuan luas.
S1
Diketahui dengan koordinat titik , , dan berturut-turut adalah , , dan . Luas adalah … satuan luas.
S2
Diketahui koordinat titik sudut segiempat berturut-turut adalah , , , dan . Luas segiempat adalah … satuan luas.
S3
Diketahui segiempat dengan titik , , , dan . Luas bidang adalah … satuan luas.
S4
Diketahui segiempat beraturan dengan titik , , , dan . Luas segiempat tersebut adalah … satuan luas.
S5
Diketahui titik sudut layang-layang adalah , , , dan . Luas layang-layang tersebut adalah … satuan luas.
S6
Diketahui koordinat titik sudut segiempat berturut-turut adalah , , , dan . Keliling segiempat adalah … satuan.
S7
Diketahui titik sudut persegipanjang adalah , , , dan . Keliling persegipanjang tersebut adalah … satuan.
S8
Diketahui dengan titik , , dan . Keliling segitiga tersebut adalah … satuan.
S9
Diketahui titik sudut layang-layang adalah , , , dan . Keliling layang-layang tersebut adalah … satuan.
S10
Diketahui segilima , dengan titik , , , , dan . Keliling bangun segilima tersebut adalah … satuan.
