Contoh Soal Konsep limit dalam konteks nyata
Contoh Soal Konsep limit dalam konteks nyata - Pada topik sebelumnya, kalian telah belajar mengenal konsep limit fungsi, sedangkan dalam topik ini kalian akan belajar tentang penerapan konsep limit dalam konteks nyata.
Mari kita ingat kembali konsep limit fungsi.
Pengertian Limit
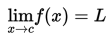
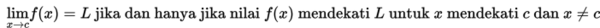
Apakah kalian masih ingat dengan limit kanan dan limit kiri?
Limit Kanan

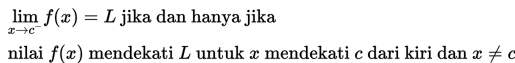
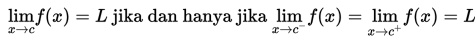
Limit Fungsi di tak hingga
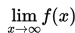

Sifat - Sifat Limit
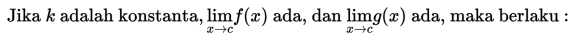

Konsep limit dalam konteks nyata diantaranya dapat dijumpai dalam bidang fisika dan ekonomi.
Penerapan limit dalam bidang fisika
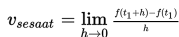
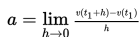
Penerapan limit dalam bidang ekonomi
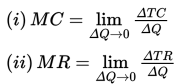
Mari kita cermati contoh berikut ini.
Contoh :

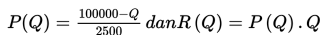
Mari kita ingat kembali konsep limit fungsi.
Pengertian Limit
Limit berarti pendekatan. Limit fungsi f(x) untuk x mendekati c sama artinya dengan pendekatan nilai f(x) untuk x = c. Selanjutnya, limit fungsi ini ditulis seperti berikut :
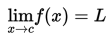
Secara intuitif, jika f : R → R , L dan c merupakan bilangan real, maka berlaku hubungan sebagai berikut :
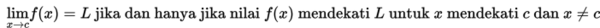
Apakah kalian masih ingat dengan limit kanan dan limit kiri?
Limit Kanan

Limit Kiri
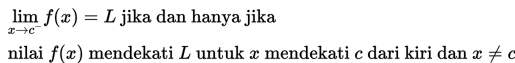
Jika diberikan fungsi f : R → R dengan L dan c bilangan real, maka berlaku pula konsep limit kanan dan limit kiri berikut ini :
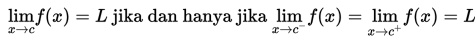
Selanjutnya, untuk menyelesaikan limit fungsi aljabar, digunakan metode berikut :
- substitusi langsung
- faktorisasi
- menyederhanakan
Limit Fungsi di tak hingga
Limit fungsi f(x) untuk x mendekati tak hingga ditulis seperti berikut :
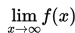
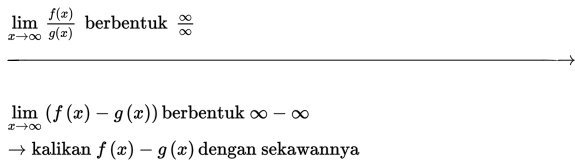
Seperti yang telah kalian ketahui, dalam limit fungsi di tak hingga, berlaku hubungan sebagai berikut :

Adapun cara untuk menyelesaikan limit fungsi di tak hingga adalah sebagai berikut :

Sifat - Sifat Limit
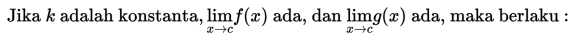

Konsep limit dalam konteks nyata diantaranya dapat dijumpai dalam bidang fisika dan ekonomi.
Penerapan limit dalam bidang fisika
Kecepatan sesaat adalah limit dari kecepatan ata-rata dan dapat dinyatakan seperti berikut ini :
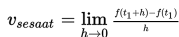
Percepatan gerak benda adalah limit dari percepatan rata-rata dan dinyatakan seperti berikut
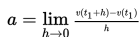
Penerapan limit dalam bidang ekonomi
Konsep limit dalam bidang ekonomi sering digunakan untuk menentukan biaya marjinal (marginal cost) dan penerimaan marjinal (marginal revenue).
Biaya marjinal adalah laju perubahan sesaat biaya terhadap banyaknya barang yang dihasilkan, sedangkan penerimaan marjinal adalah laju perubahan sesaat penerimaan terhadap banyaknya barang yang dihasilkan.
Biaya marjinal dan penerimaan marjinal dinyatakan sebagai berikut :
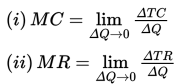
Mari kita cermati contoh berikut ini.
Contoh :
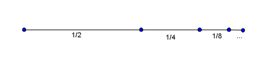
Seutas tali dengan panjang satu satuan panjang, dipotong menjadi 2 bagian yang sama, lalu ½ bagian dari tali itu dibagi 2 lagi, kemudian ¼ bagian dari tali itu dipotong menjadi 2 lagi, dan seterusnya. Apa yang dapat kamu simpulkan?
Penyelesaian :


Jika tali tersebut dipotong terus menerus, dengan panjang potongan berikutnya adalah setengah kali potongan semula, maka berdasarkan nilai limit di atas, tali tersebut pada akhirnya akan habis dan tidak lagi dapat dipotong.
S1
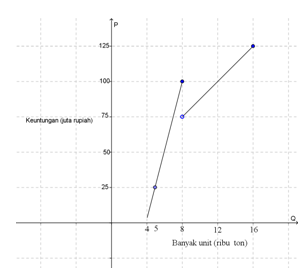
Grafik berikut ini merupakan grafik keuntungan dari produksi harian Q ton produk briket dari UKM (Usaha Kecil Menengah) di suatu kota. Nilai limit fungsi keuntungan produksi tersebut untuk Q mendekati 5 ton adalah ....

S2
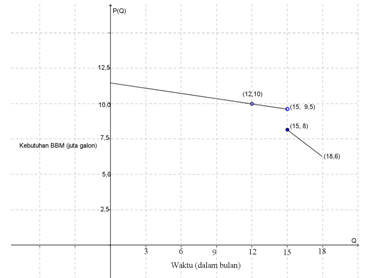
Grafik berikut ini menunjukkan kebutuhan BBM (bahan bakar minyak) di suatu daerah saat harga mengalami kenaikan harga. Diandaikan, ketika harga BBM naik, tingkat kebutuhan masyarakat akan menurun secara perlahan. Jika harga BBM berlanjut naik, tingkat kebutuhan masyarakat dapat turun sangat drastis. Besar kebutuhan BBM saat mendekati bulan yang ke-12 adalah ....

S3
Sebuah tongkat panjangnya 1 meter dipotong menjadi 3 bagian yang sama, lalu 1/3 bagian tongkat itu dipotong menjadi 3 bagian yang sama lagi, kemudian 1/9 bagian tongkat itu dibagi 3 lagi, dan seterusnya. Panjang tongkat paling pendek adalah ....
S4
Fungsi permintaan suatu produk dirumuskan
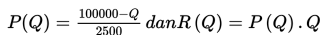
dengan
- P(Q) = harga produk
- Q = banyaknya produk
- R(Q) = Total penerimaan (TR = total revenue)
Total penerimaan marjinal ketika Q = 25 adalah ....
S5
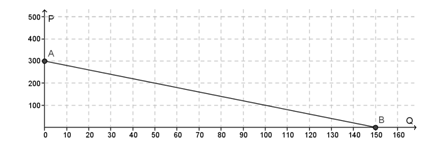
Grafik berikut ini merupakan grafik fungsi permintaan untuk produksi batik kayu.

P = harga barang per unit (dalam ratus rupiah)
Q = jumlah barang (dalam unit)
Q = jumlah barang (dalam unit)
Harga satuan batik kayu saat banyak barang mendekati 50 unit adalah ....
S6
Suatu perusahaan alat musik tradisional menjual produknya dengan rumus fungsi penawaran berikut.
P = 1000Q + 10000
Jika Q adalah banyak barang dan P adalah harga satuan barang, maka harga satuan alat musik tersebut saat banyak barang mendekati 50 unit adalah ....
S7
Sebuah mobil bergerak sepanjang jalan lurus dengan persamaan gerak s = f(t) = 3t2 (s dalam km dan t dalam jam). Kecepatan sesaat mobil itu sesudah 10 jam dari saat bergerak adalah ....
S8
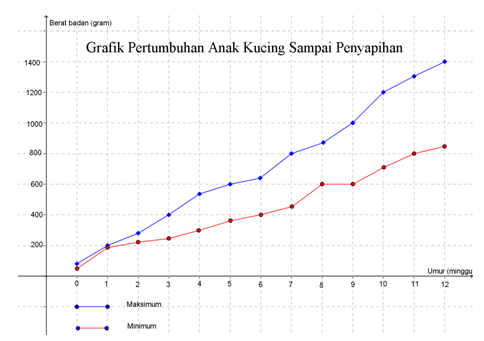
Grafik berikut ini adalah grafik pertumbuhan anak kucing dari kelahiran sampai penyapihan.

Berat badan maksimum anak kucing disekitar umur 9 minggu adalah ....
S9
Sebuah roket ditembakkan vertikal ke atas dengan persamaan gerak s = 150t – t2 dengan s dalam meter dan t dalam detik. Kecepatan sesaat roket itu setelah 3 detik ditembakkan adalah .... m/det.
S10
Sebuah perusahaan menaksir biaya memproduksi x unit mesin fotokopi (dalam $) adalah
C(Q) = 10000 + 5Q + 0,01Q2 . Biaya marjinal produk tersesebut untuk 100 unit adalah ....
C(Q) = 10000 + 5Q + 0,01Q2 . Biaya marjinal produk tersesebut untuk 100 unit adalah ....
