Contoh Soal Limit Fungsi Aljabar yang Berbentuk lim f(x) dengan x Menuju Tak Hingga
Contoh Soal Limit Fungsi Aljabar yang Berbentuk lim f(x) dengan x Menuju Tak Hingga - Pada topik sebelumnya, kalian telah mempelajari limit fungsi aljabar yang berbentuk
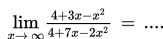
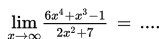
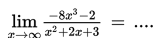
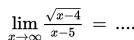
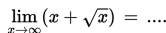
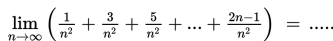
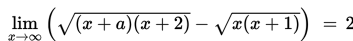
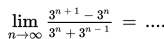
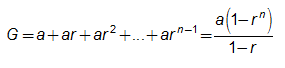
. Untuk menentukan limit tersebut, kalian menggunakan cara substitusi langsung. Substitusi langsung yang dimaksud adalah seolah-olah peubah x dalam fungsi f (x) disubstitusi langsung dengan c. Benar bukan? Tentu kalian masih mengingatnya dengan baik. Lantas, bagaimana jika x mendekati suatu bilangan yang sangat besar sekali? Untuk tahu jawabannya, yuk simak topik ini.
Pada topik ini, kalian akan belajar menentukan limit fungsi aljabar yang berbentuk . Lambang ∞ digunakan untuk menyatakan bilangan yang sangat besar sekali dan dibaca “tak hingga”. Oleh karena itu, “tak hingga” tidak boleh diperlakukan sebagai suatu bilangan yang dapat dioperasikan mengikuti kaidah aljabar bilangan biasa. Misalnya, bentuk seperti ∞ - ∞ = 0 dan adalah tidak sah, sehingga hasilnya juga tidak benar.
Limit fungsi aljabar jika x mendekati tak hingga di antaranya adalah dan .
- jika diselesaikan dengan cara substitusi langsung akan menghasilkan yang merupakan bentuk tak tentu. Untuk itu, harus diselesaikan dengan cara membagi bagian pembilang f (x) dan bagian penyebut g (x) dengan xn, n adalah pangkat tertinggi dari peubah pada pembilang f (x) atau pada penyebut g (x).
- jika diselesaikan dengan cara substitusi langsung akan menghasilkan ∞ - ∞ yang merupakan bentuk tak tentu. Untuk itu, harus diselesaikan dengan cara mengalikan dengan bentuk sekawannya, yaitu sehingga didapat . Selanjutnya, diselesaikan dengan cara membagi bagian pembilang dan bagian penyebut dengan xn , n adalah pangkat tertinggi dari peubah pada pembilang f (x) atau pada penyebut g (x).
SOAL 1
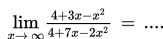
SOAL 2
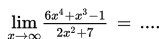
SOAL 3
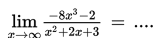
SOAL 4
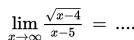
SOAL 5
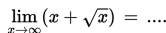
SOAL 6
Untuk n bilangan asli,
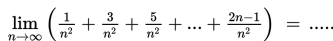
SOAL 7
Jika
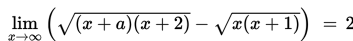
maka a = ....
SOAL 8
Jika diketahui:
maka = ....
SOAL 9
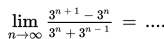
SOAL 10
Diketahui
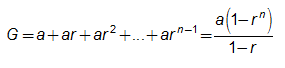
Jika -1 < r < 1, maka = ..
