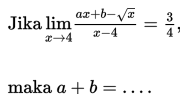Contoh Soal Limit Fungsi Aljabar yang Berbentuk lim f(x) dengan x Menuju c
Contoh Soal Limit Fungsi Aljabar yang Berbentuk lim f(x) dengan x Menuju c - Misalkan fungsi yang digambarkan Kevin Tara grafiknya adalah fungsi f (x) =

Dari tabel tersebut, tampak bahwa nilai fungsi f (x) = mendekati 0 jika x mendekati -1 baik dari arah kiri maupun dari arah kanan. Nilai fungsi f (x) untuk x mendekati suatu titik tertentu ini disebut limit fungsi tersebut. Jadi, = 0. Dibacanya, limit fungsi f (x) = adalah 0 untuk x mendekati –1. Artinya, jika x dekat dengan –1 tetapi tidak sama dengan –1, maka nilai f (x) sama dengan 0.
Pada topik kali ini, kamu akan dijelaskan cara menentukan limit fungsi aljabar seperti yang dikerjakan Kevin Tara tersebut. Namun dengan cara lain yang lebih efektif, yaitu dengan cara substitusi langsung. Substitusi langsung yang dimaksud adalah seolah-olah peubah x dalam fungsi f (x) disubstitusi langsung dengan c. Dalam pengerjaannya, kamu seringkali menjumpai kasus-kasus berikut.
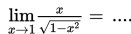
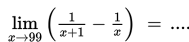

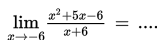
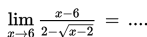
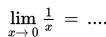
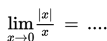
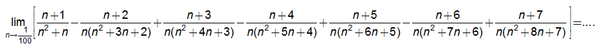
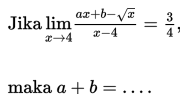
. Ia coba menentukan nilai fungsi itu untuk x mendekati -1. Nilai fungsi f (x) untuk x = -1 adalah
f (-1) = = yang merupakan suatu bentuk tak tentu. Apakah untuk x mendekati x = -1 nilai fungsi f (x) = juga? Kevin Tara coba menentukannya dengan menggunakan tabel seperti yang telah ia pelajari di SMP. Perhatikan tabel nilai-nilai f (x) untuk x mendekati -1 tersebut.
f (-1) = = yang merupakan suatu bentuk tak tentu. Apakah untuk x mendekati x = -1 nilai fungsi f (x) = juga? Kevin Tara coba menentukannya dengan menggunakan tabel seperti yang telah ia pelajari di SMP. Perhatikan tabel nilai-nilai f (x) untuk x mendekati -1 tersebut.

Dari tabel tersebut, tampak bahwa nilai fungsi f (x) = mendekati 0 jika x mendekati -1 baik dari arah kiri maupun dari arah kanan. Nilai fungsi f (x) untuk x mendekati suatu titik tertentu ini disebut limit fungsi tersebut. Jadi, = 0. Dibacanya, limit fungsi f (x) = adalah 0 untuk x mendekati –1. Artinya, jika x dekat dengan –1 tetapi tidak sama dengan –1, maka nilai f (x) sama dengan 0.
Dalam menentukan limit fungsi ini sebenarnya Kevin Tara telah menggunakan teorema limit kiri-limit kanan yang telah kita pelajari pada topik sebelumnya, yaitu:
Teorema Limit Kiri-Limit Kanan
Misalkan fungsi f (x) didefinisikan di sekitar x = c, maka jika dan hanya jika . biasa disebut limit kiri dan biasa disebut limit kanan.
Pada topik kali ini, kamu akan dijelaskan cara menentukan limit fungsi aljabar seperti yang dikerjakan Kevin Tara tersebut. Namun dengan cara lain yang lebih efektif, yaitu dengan cara substitusi langsung. Substitusi langsung yang dimaksud adalah seolah-olah peubah x dalam fungsi f (x) disubstitusi langsung dengan c. Dalam pengerjaannya, kamu seringkali menjumpai kasus-kasus berikut.
a. f (c) = h berarti
b. f (c) = berarti
c. f (c) = berarti
d. f (c) = . merupakan bentuk tak tentu. Dalam penyelesaiannya, kamu harus mencari faktor persekutuan yang sama antara bagian pembilang dan penyebut. Setelah diperoleh faktor yang sama, kemudian bentuk tersebut disederhanakan. Selain itu, kamu dapat juga mengalikan pembilang atau penyebut dengan sekawannya sehingga f (c) ≠ .
SOAL 1
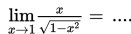
SOAL 2
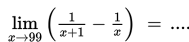
SOAL 3

SOAL 4
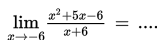
SOAL 5
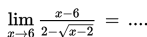
SOAL 6
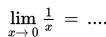
SOAL 7
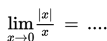
SOAL 8
Nilai dari
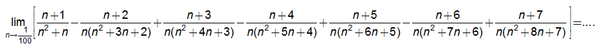
SOAL 9
Jika ,
nilai dari adalah ..
SOAL 10