Contoh Soal Persamaan Garis Singgung pada Kurva

Contoh Soal Persamaan Garis Singgung pada Kurva - Pada topik sebelumnya, kalian telah belajar tentang konsep turunan. Kalian masih mengingatnya, kan? Pemahaman kalian tentang konsep tersebut akan sangat membantu kalian dalam memahami topik kali ini, yaitu persamaan garis singgung pada sebuah kurva. Agar kalian dapat memahaminya, yuk simak topik ini dengan saksama.

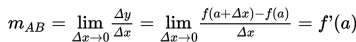
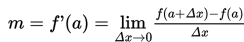
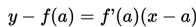
◘◘◘◘◘ Gradien Garis Singgung pada Kurva ◘◘◘◘◘

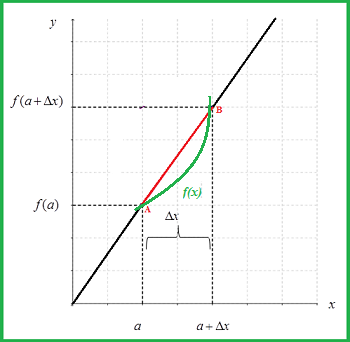
Perhatikan grafik di bawah ini.

        Pada gambar di atas, misalnya titik A adalah sebuah titik tetap yang berada pada grafik y = f(x). Titik B adalah sebuah titik yang dapat berpindah-pindah sepanjang kurva y = f(x). Jika koordinat titik A adalah A(a, f(a)) dan koordinat titik B adalah B(a + ∆x, f(a + ∆x)), bagaimana cara menentukan gradien garis singgungnya?

        Di kelas VIII SMP, kalian telah belajar cara menentukan gradien garis lurus. Gradien kalian pahami sebagai kemiringan suatu garis yang dapat ditentukan dengan membagi ∆y dengan ∆x. Pada gambar di atas, Jika titik B bergerak mendekati titik A sepanjang kurva y = f(x), maka ∆x akan semakin kecil. Untuk ∆x mendekati nol, maka tali busur AB menjadi garis singgung kurva y = f(x) pada titik A. Hal ini dinyatakan dengan:

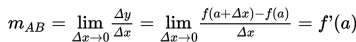
        Sebagaimana yang telah kalian pelajari pada konsep turunan, bentuk turunan fungsi seperti inilah yang nantinya akan banyak kalian gunakan dalam topik kali ini, yaitu:

Misalkan f(x) = axn dengan a adalah bilangan real dan n bilangan bulat positif, maka f '(x) = naxn-1.

        Nah, jika kalian telah paham dengan konsep-konsep tersebut, mari kita ingat kembali ketentuan gradien pada dua garis sejajar dan garis tegak lurus berikut.

• Pada dua garis yang saling sejajar, berlaku m1 = m2
• Pada dua garis yang saling tegak lurus, berlaku m1 x m2 = -1

        Tentu kalian telah paham tentang gradien garis singgung pada kurva, kan? Pemahaman kalian tentang materi tersebut akan kalian gunakan untuk mempelajari materi berikut.

◘◘◘◘◘ Persamaan Garis Singgung pada Kurva ◘◘◘◘◘

Apakah kalian masih ingat persamaan garis lurus dengan gradien m dan melalui titik P(x1, y1)?

Persamaan garis lurus dengan gradien m dan melalui titik P(x1, y1) adalah:

                                             y - y1 = m(x - x1)

Gradien garis singgung kurva y = f(x) pada titik (a, f(a)) adalah:

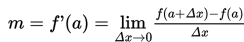
Dengan demikian, persamaan garis singgung sebuah garis y = f(x) pada titik (a, f(a)) adalah:

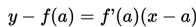
dengan:

a = x1

f(a) = y1

f '(a) = m

SOAL 1

Gradien garis singgung kurva f(x) = 2x2 + 5x di sebuah titik dengan absis 2 adalah ….

SOAL 2

Koordinat titik singgung kurva f(x) = x2 + 34$\frac{3}{4}$ agar gradiennya 9 adalah ….

SOAL 3

Persamaan garis singgung kurva jika diketahui f(x) = 2x2 di titik A(2, 8) adalah ….

SOAL 4

Persamaan garis singgung kurva jika diketahui f(x) = 2x2 + 3x + 1 di titik P(0, 1) adalah …

SOAL 5

Persamaan garis singgung kurva jika diketahui f(x) = x2 + 2x di titik x = 12$\frac{1}{2}$ dan x = 1 adalah ….

SOAL 6

Jika diketahui f '(x) = 4x - 1 di titik P(2, 6), maka persamaan garis singgung kurva y = f(x) adalah ….

SOAL 7

Persamaan garis singgung sebuah kurva f(x) = x2+ 14x$\frac{1}{4}x$ + 1 adalah y = 174x−3$\frac{17}{4}x-3$. Koordinat titik singgung kurva tersebut adalah ….

SOAL 8

Persamaan garis singgung kurva f(x) = 4x2 yang sejajar dengan garis y = 2x + 1 adalah ….

SOAL 9

Persamaan garis singgung kurva f(x) = 3x3 + 1 yang tegak lurus dengan garis y = −19$-\frac{1}{9}$ x + 3 pada titik absis positif adalah …

SOAL 10

Sebuah garis y = x + 8 memotong kurva y = 2x2 + 3x + 4 di titik A dan B. Persamaan garis singgung kurva di titik A dan titik B adalah ....

Share this post