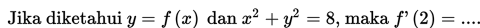Contoh Soal Aturan Rantai untuk Mencari Turunan Fungsi

Contoh Soal Aturan Rantai untuk Mencari Turunan Fungsi - Kamu sudah memahami bahwa turunan suatu fungsi didapat dengan memanfaatkan definisi turunan fungsi yaitu,

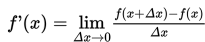
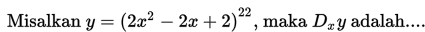
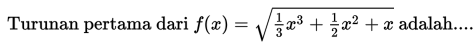
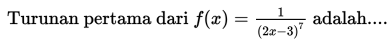
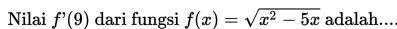
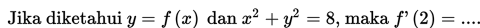
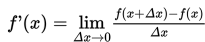
Penggunaan definisi tersebut cenderung mudah untuk fungsi tunggal yang sederhana, tetapi penggunaaanya menjadi lebih rumit, memakan waktu lama dan tentunya melelahkan apabila kamu diminta untuk menentukan turunan dari fungsi yang berderajat besar seperti f (x) = (x2 + x + 1)100 . Dengan menggunakan definisi, mula-mula kamu harus menjabarkan f (x) ke dalam suatu suku banyak berderajat 200, kemudian mencari turunan dari setiap suku yang ada satu per satu.

       Setelah mempelajari topik ini, kamu tidak perlu khawatir jika diminta untuk menentukan turunan fungsi berderajat besar karena kamu akan mempelajari suatu metode (prosedur) penentuan turunan fungsi yang lebih ‘canggih’ dibanding metode-metode sebelumnya. Prosedur ini pertama kali diperkenalkan oleh seorang matematikawan Jerman bernama Gottfried Wilhelm Leibniz (1646-1716) yang dikenal dengan nama Aturan Rantai. 

       Sebelum kamu mempelajari aturan rantai, ada baiknya kamu mengenal terlebih dahulu notasi-notasi turunan fungsi.

Notasi Turunan Fungsi

Dalam penerapan aturan rantai, pemilihan notasi memainkan peranan yang cukup penting dalam penyederhanaan tampilan dari perhitungan yang akan dilakukan. Untuk suatu fungsi y = f (x) ada beberapa notasi yang lazim digunakan. Adapun notasi-notasi tersebut adalah.

• f' (x) merupakan Notasi Lagrange untuk menyatakan turunan pertama dari f (x) terhadap x.
• dydx$\frac{dy}{dx}$ merupakan Notasi Leibniz untuk menyatakan turunan pertama dari fungsi y terhadap x.
• Dxy$D_{x}y$ merupakan Notasi Euler untuk menyatakan turunan pertama dari fungsi y terhadap x.

        Dalam pembelajaran kali ini ketiga notasi di atas akan digunakan dalam contoh soal dan soal latihan. Notasi Lagrange dan Leibniz lebih umum digunakan. Namun, kamu boleh memilih notasi yang kamu anggap paling sederhana. 

Aturan Rantai

Misalkan y = f (u) dan u = g (x), y memiliki turunan di u dan u memiliki turunan di x sehingga, fungsi komposisi y = (f o g) (x) = f (g (x)) memiliki turunan di x yaitu,

(f o g)' (x) = f' (g (x)) . g' (x)

atau
dydx$\frac{dy}{dx}$ = dydu$\frac{dy}{du}$ . dudx$\frac{du}{dx}$

atau bisa pula dipahami sebagai,
Dxy$D_{x}y$ = Dxy$D_{x}y$

Dalam bahasa yang lebih sederhana, aturan rantai menyatakan bahwa turunan fungsi komposisi ditentukan dengan mengalikan fungsi terluar yang diturunkan terhadap fungsi di dalam (f’ (g (x)) dengan turunan dari fungsi di dalam (g’(x)). 

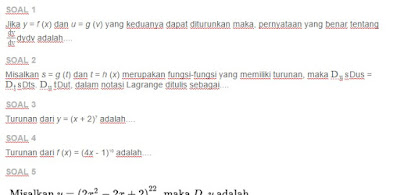
SOAL 1

Jika y = f (x) dan u = g (v) yang keduanya dapat diturunkan maka, pernyataan yang benar tentang dydv$\frac{dy}{dv}$ adalah....

SOAL 2

Misalkan s = g (t) dan t = h (x) merupakan fungsi-fungsi yang memiliki turunan, maka Dus$D_{u}s$ = Dts$D_{t}s$. Dut$D_{u}t$, dalam notasi Lagrange ditulis sebagai....

SOAL 3

Turunan dari y = (x + 2)7 adalah....

SOAL 4

Turunan dari f (x) = (4x - 1)10 adalah....

SOAL 5

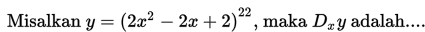
SOAL 6

Turunan pertama dari f' (x) = ((x - 2) (x + 2))4terhadap x adalah....

SOAL 7

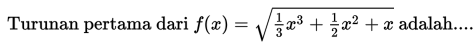
SOAL 8

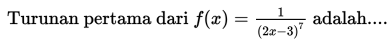
SOAL 9

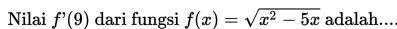
SOAL 10

Share this post