Contoh Soal Memahami Persamaan Linier Dua Variabel
Contoh Soal Memahami Persamaan Linier Dua Variabel - Persamaan linear dua variabel seringkali digunakan untuk memecahkan permasalahan di sekitar kita. Sebelum kita mempelajari persamaan linear dua variabel, sebaiknya kita perhatikan permasalahan berikut ini.
Dian hendak membeli buah yang terdiri dari jeruk dan pisang. Banyaknya buah yang akan dibeli sebanyak 10 buah. Jika kita mendaftar banyaknya jeruk dan pisang yang akan dibeli, kita bisa menggunakan tabel berikut ini.

Mari kita perhatikan definisi dari persamaan linear dua variabel.
Persamaan linear dua variabel dapat dituliskan dalam bentuk ax + by = c di mana a, b, dan c adalah bilangan real dan a, b keduanya tidak sama dengan nol.
Penyelesaian :
Lalu, bagaimana cara menggambarkan penyelesaian (x,y)?
Penyelesaian :
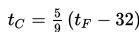
Dian hendak membeli buah yang terdiri dari jeruk dan pisang. Banyaknya buah yang akan dibeli sebanyak 10 buah. Jika kita mendaftar banyaknya jeruk dan pisang yang akan dibeli, kita bisa menggunakan tabel berikut ini.

Jika dituliskan dalam sebuah persamaan, permasalahan di atas dapat dituliskan sebagai :
j + p = 10 dengan j adalah banyak jeruk dan p adalah banyak pisang.
j + p = 10 dengan j adalah banyak jeruk dan p adalah banyak pisang.
Mari kita perhatikan definisi dari persamaan linear dua variabel.
Persamaan linear dua variabel dapat dituliskan dalam bentuk ax + by = c di mana a, b, dan c adalah bilangan real dan a, b keduanya tidak sama dengan nol.
Berikut ini adalah beberapa contoh persamaan linear dua variabel :
- 2x + 5y = 8
- -3a + b = 7
- 2(p - 8) = q + 9
Penyelesaian dari persamaan linear dua variabel dituliskan dalam bentuk pasangan berurutan (x,y). Untuk lebih jelasnya, mari kita cermati contoh berikut :
Tentukan apakah pasangan berurutan berikut merupakan penyelesaian dari persamaan
2x + 3y = 24
2x + 3y = 24
a) (6,4)
b) (8,2)
b) (8,2)
Penyelesaian :
a) Penyelesaian dari persamaan linear dua variabel adalah pasangan berurutan (x,y). Dengan demikian, (6,4) mempunyai arti bahwa x = 6 dan y = 4.
Selanjutnya, untuk mengetahui apakah (6,4) merupakan penyelesaian dari 2x + 3y = 24, mari kita substitusikan x = 6 dan y = 4 ke persamaan tersebut.
2x + 3y = 24
<=> 2(6) + 3(4) = 24
<=>12 + 12 = 24
<=> 24 = 24 ... (benar)
<=> 2(6) + 3(4) = 24
<=>12 + 12 = 24
<=> 24 = 24 ... (benar)
Karena hasil substitusi bernilai benar, maka (6,4) merupakan penyelesaian dari 2x + 3y = 24.
b) Pasangan berurutan (8,2) mempunyai arti x = 8 dan y = 2. Jika kita subtitusikan nilai x dan y ke persamaan, maka diperoleh :
2x + 3y = 24
<=> 2(8) + 3(2) = 24
<=> 16 + 6 = 24
<=> 22 = 24 ... (salah)
<=> 2(8) + 3(2) = 24
<=> 16 + 6 = 24
<=> 22 = 24 ... (salah)
Karena hasil substitusi bernilai salah, maka (8,2) bukan penyelesaian dari 2x + 3y = 24.
Lalu, bagaimana cara menggambarkan penyelesaian (x,y)?
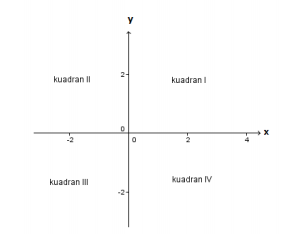
Penyelesaian persamaan linear dua variabel dapat dapat digambarkan dengan sistem koordinat kartesius. Pada sistem koordinat kartesius, garis horizontal disebut sumbu x dan garis vertikal disebut sumbu y. Sumbu x dan y membagi bidang koordinat menjadi 4 kuadran dan perpotongannya disebut titik O (origin).

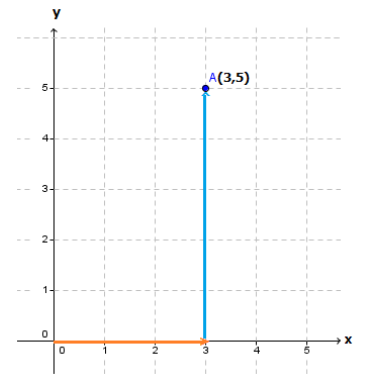
Misalkan kita akan menggambarkan A(3,5) pada bidang koordinat. Nilai x titik A adalah 3 atau absis titik A adalah 3, sedangkan nilai y dari titik A adalah 5 atau ordinat titik A adalah 5. Dengan demikian, dari titik O(0,0) , kita bergerak 3 satuan ke kanan kemudian bergerak 5 satuan ke atas.

Mari kita cermati salah satu permasalahan dari persamaan linear dua variabel.
Seorang pengusaha warnet menyewakan, komputer dengan biaya sewa Rp 3.000,00 ditambah Rp 1.000,00 per jam. Jika x menyatakan jam dan y menyatakan biaya sewa, maka permasalahan di atas dapat ditulis dalam bentuk persamaan :
y = 3.000 + 1.000x = 1.000x + 3.000
Jika Adi akan menyewa komputer selama 3 jam, berapakah biaya sewa yang harus dibayarkan?
Penyelesaian :
Adi menyewa komputer selama 3 jam, artinya x = 3 sehingga
y = 1.000(3) + 3.000 = 3.000 + 3.000 = 6.000
y = 1.000(3) + 3.000 = 3.000 + 3.000 = 6.000
Jadi, biaya sewa yang harus dibayarkan Adi adalah Rp 6.000,00.
S1
Persamaan berikut ini yang merupakan persamaan linear dua variabel adalah ....
S2
Pasangan berurut berikut yang merupakan penyelesaian persamaan 2x + 6y = 10 adalah ....
S3
Jika (5,t) merupakan penyelesaian persamaan 3x - y = 4, nilai t adalah ....
S4
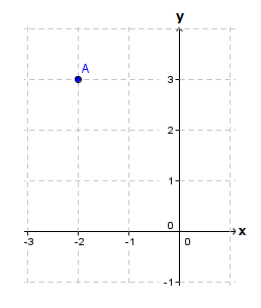
Perhatikan gambar di bawah ini!

Koordinat titik A adalah ....
S5
Tarif parkir mobil di stasiun Tugu adalah Rp 5.000,00 untuk jangka waktu 10 jam. Jika melebihi batas tersebut, maka pemarkir harus membayarkan tambahan biaya Rp 1.000,00 per jam. Jika x menyatakan waktu (jam) dan y menyatakan tarif parkir, maka persamaan yang sesuai dengan masalah tersebut adalah ....
S6
Dini bersepeda dari rumahnya di Bantul menuju Jogja. Jarak dari rumah Dini ke Jogja dinyatakan dengan persamaan y = 75x, dengan x menyatakan banyaknya waktu yang diperlukan (dalam menit) dan y menyatakan jarak tempuh (dalam meter).
Jarak tempuh Dini akan mencapai 1,5 kilometer jika ia bersepeda selama ... menit.
S7
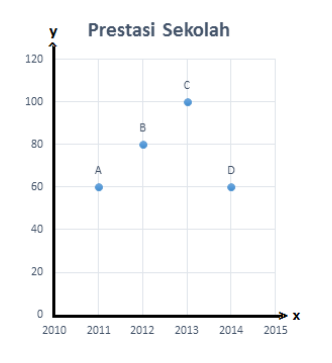
Grafik di bawah menyatakan banyaknya prestasi yang dicapai suatu sekolah dari tahun 2011 sampai dengan tahun 2014.

Pada grafik di atas, sumbu x menyatakan tahun dan sumbu y menyatakan banyaknya prestasi. Banyaknya prestasi pada tahun 2013 adalah ...
S8
Tarif sebuah taksi di sebuah kota adalah sebagai berikut: tarif kilometer pertama adalah Rp 8.000,00 kemudian pada per kilometer berikutnya tarifnya adalah Rp 2.000,00. Persamaan yang bersesuaian dengan masalah tersebut adalah ...
S9
Di Amerika menggunakan skala Fahrenheit untuk mengukur suhu, sedangkan Indonesia biasa menggunakan skala Celcius. Hubungan antara skala Celcius dan Fahrenheit adalah
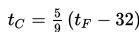
dengan tC adalah suhu dalam Celsius dan tF adalah suhu dalam Fahrenheit. Jika diketahui suhu udara 25oC, maka suhu tersebut dalam skala Fahrenheit adalah ....
S10
Seorang petani membeli 2 pohon markisa dan 5 pohon mangga seharga Rp 300.000,00. Jika x menyatakan harga pohon mangga dan y menyatakan harga pohon markisa., maka persamaan linear dua variabel yang bersesuaian dengan permasalahan tersebut adalah ....
