Contoh Soal Menyelesaikan Sistem Persamaan Linier Dua Variabel

Contoh Soal Menyelesaikan Sistem Persamaan Linier Dua Variabel - Pada topik sebelumnya kita telah berkenalan dengan persamaan linear dua variabel.

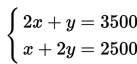
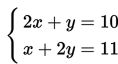
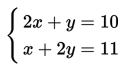
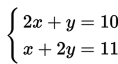
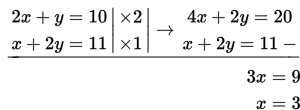
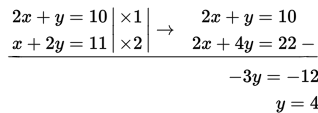
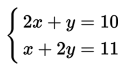
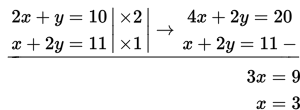
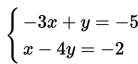
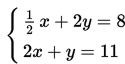
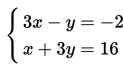
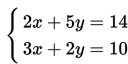
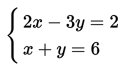
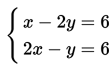
Nah, pada topik kali ini kita akan mempelajari tentang penyelesaian sistem persamaan linear dua variabel serta contoh penggunaannya dalam permasalahan nyata.

Untuk lebih memahami tentang sistem persamaan linear dua variabel, mari kita simak permasalahan berikut ini.
Anto membeli dua buah pensil dan sebuah penghapus dengan harga Rp 3.500,00. Hari berikutnya ia membeli sebuah buku dan dua buah penghapus yang sama di toko yang sama pula seharga Rp 2.500,00. Berapakah harga masing-masing sebuah buku tulis dan sebuah penggaris?

Masalah di atas dapat diselesaikan dengan terlebih dahulu membuat suatu permisalan sebagai berikut.

Misal :
x = harga sebuah pensil
y = harga sebuah penggaris

Sehingga permasalahan di atas dapat dinyatakan dalam bentuk sistem persamaan linear dua variabel berikut ini:

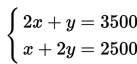
Harga masing-masing sebuah buku tulis dan sebuah penggaris dapat ditentukan dengan menentukan nilai pasangan berurutan (x,y) yang memenuhi kedua persamaan itu secara serentak.
Terdapat beberapa metode untuk menentukan penyelesaian suatu sistem persamaan linear dua variabel, yaitu :
1. Metode grafik
2. Metode subtitusi
3. Metode eliminasi
4. MetodeGabungan (eliminasi dan substitusi)

Mari kita simak satu-persatu metode-metode penyelesaian tersebut.

1. Metode Grafik

Grafik persamaan linear dua variabel berupa garis lurus, sehingga grafik suatu sistem persamaan linear dua variabel berupa dua buah garis lurus.
Pasangan titik (x,y) yang merupakan titik potong kedua garis lurus tersebut adalah penyelesaian dari sistem persamaan linearnya.

Contoh :

Misal kita akan menyelesaikan sistem persamaan linear berikut ini menggunakan metode grafik.

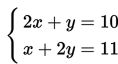
Jawab :

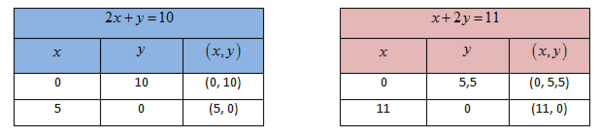
Pertama-tama kita buat tabel untuk melukiskan grafik masing-masing persamaan tersebut.

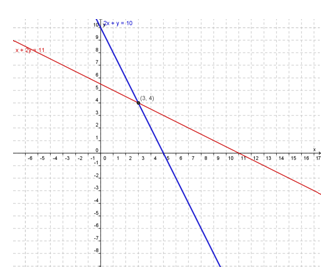
Sehingga diperoleh grafik :

Berdasarkan grafik di atas, diperoleh titik potong (3, 4).
Dengan demikian (3, 4) merupakan solusi dari sistem persamaan linear di atas.

2. Metode Subtitusi

Menyelesaikan sistem persamaan linear dua variabel dengan metode substitusi dilakukan dengan cara mengubah bentuk salah satu persamaan linear dua variabel.
Bentuk baru tersebut kemudian digunakan untuk menggantikan variabel yang sama pada persamaan linear berikutnya.
Untuk lebih jelasnya, mari kita simak contoh berikut ini.

Contoh :

Misal kita akan menyelesaikan sistem persamaan linear berikut ini menggunakan metode subtitusi.

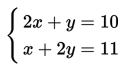
Jawab :

Mula-mula ubah salah satu persamaan sebagai berikut:
2x + y = 10 → y = 10 – 2x

Kemudian subtitusikan ke persamaan berikutnya sebagai berikut:
x + 2y = 11
x + 2(10 – 2x) = 11
x + 20 – 4x = 11
-3x + 20 = 11
-3x = -9
x = 3

Diperoleh salah satu solusi yaitu x = 3.
Selanjutnya tentukan solusi berikut nya dengan menyubstitusikan nilai x = 3 ke y = 10 – 2x.

y = 10 – 2x 
= 10 – 2(3)
= 10 – 6 
= 4

Diperoleh y = 4.
Dengan demikian diperoleh solusi sistem persamaan linear yaitu (3,4).

3. Metode Eliminasi

Menyelesaikan sistem persamaan linear dua variabel dilakukan dengan cara menghilangkan salah satu variabel untuk dapat menentukan nilai variabel yang lain.
Untuk itu, koefisien salah satu variabel yangakan dihilangkan harus sama atau dibuat sama.

Mari kita simak contoh berikut ini.

Contoh :

Misal kita akan menyelesaikan sistem persamaan linear berikut ini menggunakan metode eliminasi.

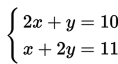
Jawab :

Mula-mula kita eliminasi variabel y terlebih dahulu :

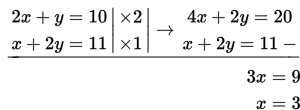
Selanjutnya, kita eliminasi variabel x:

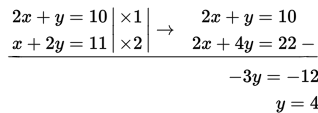
Dengan demikian diperoleh penyelesaian yaitu (3,4).

4. Metode Gabungan

Menyelesaikan sistem persamaan linear dua variabel dapat dilakukan dengan metode gabungan eliminasi dan substitusi. Langkah pertama lakukan eliminasi salah satu variabel kemudian nilai variabel yang diperoleh digunakan untuk menggantikan variabel yang sama pada salah satu persamaan linear pada sistem tersebut.

Agar lebih jelas, mari kita simak contoh berikut ini.

Contoh :

Misal kita akan menyelesaikan sistem persamaan linear berikut ini menggunakan metode gabungan eliminasi dan substitusi.

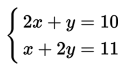
Jawab :

Mula-mula kita eliminasi variabel y terlebih dahulu :

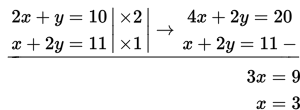
Selanjutnya, kita substitusi nilai variabel x tersebut ke salah satu persamaan linear dalam sistem ini, misalkan kita substitusikan ke 2x + y = 10 sehingga diperoleh:
2(3) + y = 10
6 + y = 10
y = 4

Dengan demikian diperoleh penyelesaian adalah (3,4).

S1

Bentuk-bentuk berikut ini yang merupakan sistem persamaan linear dua variabel adalah ….

S2

Penyelesaian dari sistem persamaan linear berikut ini adalah …

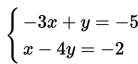
S3

Penyelesaian dari sistem persamaan linear berikut ini adalah ….

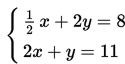
S4

Penyelesaian dari sistem persamaan linear berikut ini adalah …

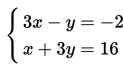
S5

Jika (x,y) adalah penyelesaian sistem persamaan linear berikut ini :

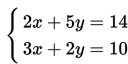
Maka x + y = ….

S6

Jika (x,y) adalah penyelesaian sistem persamaan linear berikut ini :

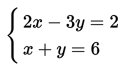
Maka x . y = …..

S7

Seorang pengrajin membuat 60 buah guci merah dan guci hijau. Biaya yang dikeluarkan untuk membuat sebuah guci merah adalah Rp 250.000,00, sedangkan biaya untuk membuat sebuah guci hijau adalah Rp 300.000,00. Total biaya yang dikeluarkan oleh pengrajin tersebut adalah Rp 16.250.000,00. Sistem persamaan linear yang dapat digunakan untuk menentukan banyaknya masing-masing jenis guci adalah …

S8

Dua kali umur kakak ditambah tiga kali umur adik adalah 60 tahun. Sedangkan tiga kali umur kakak ditambah dua kali umur adik adalah 65 tahun. Umur kakak adalah ….

S9

Jumlah dua buah bilangan adalah 50 sedangkan selisihnya adalah 14. Salah satu bilangan tersebut adalah ….

S10

Grafik berikut ini yang menunjukkan penyelesaian dari sistem persamaan linear dua variabel:

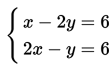
adalah …

Share this post