Contoh Soal Membuat dan Menyelesaikan Masalah yang Berkaitan dengan SPLDV
Contoh Soal Membuat dan Menyelesaikan Masalah yang Berkaitan dengan SPLDV - Masihkah kamu ingat dengan pengertian sistem persamaan linear dua variabel (SPLDV) dan metode-metode yang dapat digunakan untuk menentukan himpunan penyelesaian dari SPLDV tersebut? Marilah sejenak kita ingat kembali.
Definisi
Berdasarkan pengalaman pada saat menentukan penyelesaian SPLDV dengan metode grafik, substitusi, eliminasi atau gabungan eliminasi dan substitusi, apa metode yang paling efektif untuk menyelesaikan SPLDV?
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
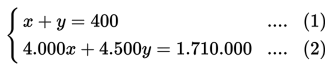
Contoh 2 :

Contoh 3 :
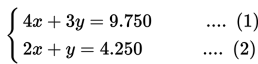
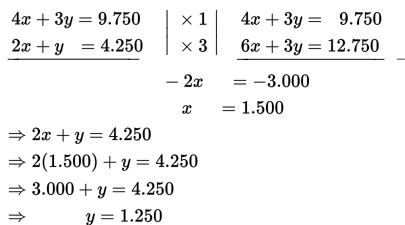
Contoh 4 :
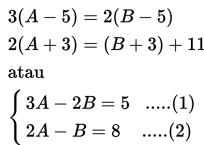
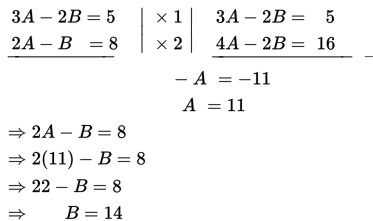
Contoh 5 :
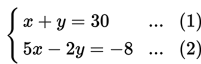
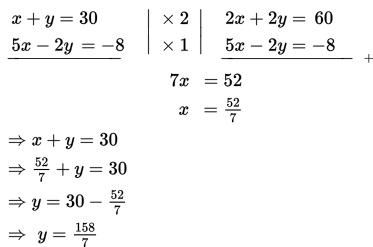
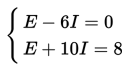
Definisi
Sistem persamaan linear dua variabel (SPLDV) adalah suatu sistem persamaan linear dengan dua variabel.
Jika kedua variabel yang dimaksud adalah x dan y, maka bentuk umum SPLDV adalah sebagai berikut :
a1x + b1y = c1 ............................................. (Persamaan-1)
a2x + b2y = c2 ............................................. (Persamaan-2)
dengan a1, a2, b1, b2, c1, dan c2 adalah bilangan real ; a1 dan b1 tidak boleh kedua-duanya nol ; a2 dan b2 tidak boleh kedua-duanya nol.
Adapun penyelesaian dari sistem persamaan linear dua variabel merupakan pasangan berurutan (x, y) yang memenuhi kedua persamaan linear tersebut sehingga memberikan pernyataan yang benar.
Ada beberapa cara dalam mencari penyelesaian sistem persamaan linear dua variabel, yaitu :
- Metode Grafik
- Metode Eliminasi
- Metode Substitusi
- Metode Gabungan (eliminasi dan substitusi)
Banyak permasalahan dalam kehidupan kita sehari-hari yang berkaitan dengan sistem persamaan linear. Dalam hal ini, kita dituntut untuk dapat mengubah persoalan tersebut dalam kalimat matematika sehingga permasalahan tersebut dapat diselesaikan dengan sistem persamaan linear dua variabel.
Berdasarkan pengalaman pada saat menentukan penyelesaian SPLDV dengan metode grafik, substitusi, eliminasi atau gabungan eliminasi dan substitusi, apa metode yang paling efektif untuk menyelesaikan SPLDV?
Benarkah metode substitusi bekerja lebih lambat dalam menemukan nilai variabel pertama, tapi sangat cepat dalam mendapatkan nilai variabel kedua setelah nilai variabel pertama diketahui?
Benarkah metode eliminasi justru cepat untuk menemukan nilai variabel pertama, tetapi justru lambat dalam menemukan nilai variabel kedua karena proses eliminasi diulang dari awal?
Kamu mungkin sudah menduga dan menemukan jawabannya. Cara terbaik menyelesaikan SPLDV adalah dengan menggabungkan metode eliminasi dan substitusi. Metode eliminasi digunakan untuk mendapatkan nilai variabel pertama dan hasilnya disubstitusikan ke persamaan untuk mendapatkan nilai variabel kedua.
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Pak Ali seorang pedagang beras. Setiap liter beras yang dijual, selalu ia campur dengan dua jenis beras berbeda yang harganya masing-masing Rp4.000,00 dan Rp4.500,00. Jumlah campuran beras yang dijual Pak Ali sebanyak 400 liter. Setelah beras habis terjual, diperoleh pendapatan sebesar Rp1.710.000,00. Berapa literkah masing-masing beras pada campuran beras tersebut?
Penyelesaian :
Misalkan banyak beras jenis I adalah x liter dan beras jenis II adalah y liter, maka diperoleh sistem persamaan :
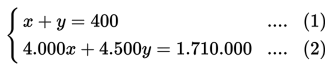
Karena x + y = 400 <=> y = 400 - x maka dengan melakukan subtitusi ke persamaan
4.000x + 4.500y = 1.710.000 diperoleh :
4.000x + 4.500y = 1.710.000 diperoleh :
4.000x + 4.500(400 - x) = 1.710.000
<=> 4.000x + 1.800.000 - 4.500x = 1.710.000
<=> 4.000x - 4.500x = 1.710.000 - 1.800.000
<=> -500x = -90.000
<=> x = 180
<=> 4.000x + 1.800.000 - 4.500x = 1.710.000
<=> 4.000x - 4.500x = 1.710.000 - 1.800.000
<=> -500x = -90.000
<=> x = 180
Selanjutnya, dengan mensubtitusikan nilai x = 180 ke persamaan y = (400 - x), diperoleh
y = 400 - 180 = 220.
y = 400 - 180 = 220.
Jadi, beras jenis I yang dicampur sebanyak 180 liter dan beras jenis II yang dicampur sebanyak 220 liter.
Contoh 2 :
Lebar persegi panjang adalah setengah panjangnya. Jika keliling persegi panjang tersebut 90 cm, maka tentukan luasnya!
Penyelesaian :
Berdasarkan informasi dalam soal, l = 1/2 p dan K = 90, sehingga dengan melakukan subtitusi kita peroleh :

Jadi, luas persegi panjang tersebut adalah 450 cm2.
Contoh 3 :
Di suatu toko Adi membeli 4 buku tulis dan 3 pensil dengan harga Rp9.750,00 dan Budi membeli 2 buku tulis dan sebuah pensil dengan harga Rp4.250,00. Jika Frida membeli 5 buku tulis dan 2 pensil, berapakah harga yang harus dibayar oleh Frida?
Penyelesaian :
Misalkan harga sebuah buku tulis x rupiah dan harga sebuah pensil y rupiah.
Masalah di atas dapat dituliskan dalam sistem persamaan sebagai berikut :
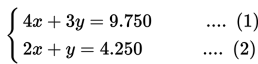
Dengan metode eliminasi-substitusi kita peroleh :
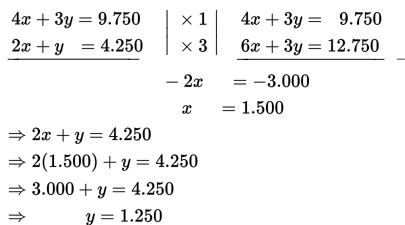
Jadi, harga sebuah buku tulis adalah Rp1.500,00 dan harga sebuah pensil adalah Rp1.250,00. Frida membeli lima buku tulis dan dua pensil, sehingga Frida harus membayar sebesar Rp10.000,00.
Contoh 4 :
Jika lima tahun lalu, 3 kali umur A sama dengan 2 kali umur B dan tiga tahun yang akan datang, 2 kali umur A sama dengan umur B ditambah 11 tahun, maka berapakah umur A dan umur B sekarang?
Penyelesaian :
Berdasarkan informasi di atas kita, peroleh SPLDV sebagai berikut :
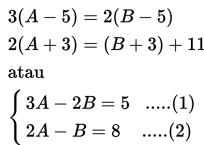
Dengan metode eliminasi-substitusi kita peroleh A dan B sebagai berikut :
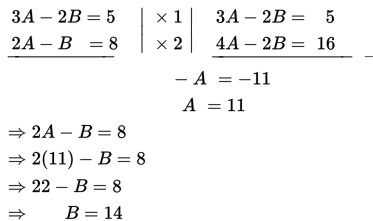
Jadi, sekarang umur A = 11 tahun dan umur B = 14 tahun.
Contoh 5 :
Dua bilangan jika dijumlahkan menghasilkan 30. Jika lima kali bilangan yang satu dikurangkan dua kali bilangan yang lain hasilnya adalah –8. Tentukan kedua bilangan itu!
Penyelesaian :
Misalkan bilangan pertama adalah x dan bilangan kedua adalah y, maka diperoleh SPLDV sebagai berikut :
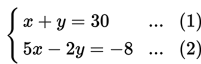
Dengan metode eliminasi-substitusi, diperoleh :
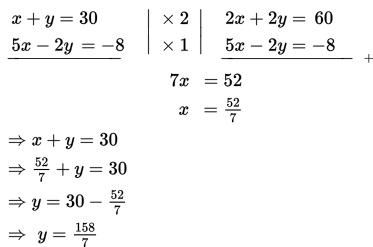
Jadi, kedua bilangan tersebut adalah 52/7 dan 158/7.
S1
Pada suatu pertunjukan wayang kulit, terjual karcis kelas I dan kelas II sebanyak 500 lembar. Harga karcis kelas I sebesar Rp10.000,00 dan karcis kelas II sebesar Rp6.000,00. Jika hasil penjualan seluruh karcis adalah Rp3.800.000,00 maka banyak masing-masing karcis kelas I dan kelas II yang terjual berturut-turut adalah ... lembar.
S2
Johan dan Ali bekerja pada sebuah konveksi membuat baju. Johan dapat membuat 4 baju setiap jamnya sedangkan Ali membuat 5 baju. Jumlah jam bekerja Johan dan Ali dalam satu hari adalah 12 jam dengan banyak baju yang dapat dibuat mereka sebanyak 53 buah. Lamanya waktu bekerja Johan dan Ali berturut-turut adalah ....
S3
Setengah uang Naufal ditambah 2/3 uang Tazkia adalah Rp30.000,00. Sedangkan 2/5 uang Naufal ditambah ½ uang Tazkia adalah Rp23.000,00. Besar uang Naufal dan Tazkia berturut-turut adalah....
S4
Jumlah dua bilangan adalah 67 dan selisihnya 13. Jika dibuat sebuah pecahan dengan pembilangnya bilangan yang kecil, maka penyebut pecahan tersebut adalah ....
S5
Penggunaan Hukum Ohm untuk rangkaian listrik diberikan oleh sistem persamaan berikut ini :
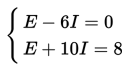
Nilai E dan I dari sistem persamaan di atas adalah ....
S6
Suatu larutan mempunyai kadar asam 25% dan larutan lainnya mengandung 65% asam. Banyaknya masing-masing larutan yang dibutuhkan untuk mendapatkan 8 liter larutan baru dengan kadar asamnya 40% adalah ....
S7
Jika pembilang dan penyebut dari suatu pecahan dikurangi dengan 5, maka pecahan itu menjadi 3/5. Jika pembilang dan penyebut masing-masing ditambah dengan 9, pecahan itu menjadi 5/6. Pecahan itu adalah ....
S8
Uang Irna sama dengan 3/2 uang Tuti. Jika jumlah uang mereka Rp35.000,00 maka uang Irna adalah ....
S9
Satu tahun yang lalu umur Budi 2 kali umur Andri, sementara 2 tahun yang akan datang umur Andri adalah 2/3 umur Budi. Umur Andri sekarang adalah ....
S10
Sebuah persegi panjang memiliki panjang 1 cm lebih dari 2 kali lebarnya. Jika keliling persegi panjang 44 cm, maka panjang persegi panjang itu adalah ....
