Contoh Soal Memahami Persamaan Kuadrat
Contoh Soal Memahami Persamaan Kuadrat - Pada topik sebelumnya, kita telah belajar mengenai bentuk aljabar dan operasi-operasinya. Nah, dalam topik kali ini kita akan memperdalam pengetahuan kita dengan mempelajari tentang persamaan kuadrat. Seperti apakah persamaan kuadrat? Mari kita simak topik berikut ini.
Bentuk Umum Persamaan Kuadrat
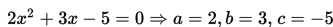
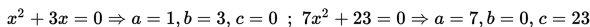
Penggunaan Diskriminan
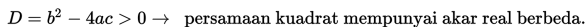



Sifat-sifat Akar Persamaan Kuadrat
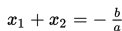
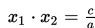
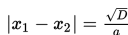
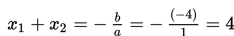
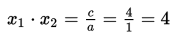
Bentuk Umum Persamaan Kuadrat
Bentuk umum persamaan kuadrat dengan variabel adalah :
ax2 + bx + c = 0
dengan a tidak sama dengan 0 dan a, b, c bilangan real.
ax2 + bx + c = 0
dengan a tidak sama dengan 0 dan a, b, c bilangan real.
Nilai x yang memenuhi persamaan ax2 + bx + c = 0 disebut akar-akar atau penyelesaian persamaan kuadrat.
Terdapat dua jenis persamaan kuadrat, yaitu persamaan kuadrat lengkap dan persamaan kuadrat tidak lengkap.
Terdapat dua jenis persamaan kuadrat, yaitu persamaan kuadrat lengkap dan persamaan kuadrat tidak lengkap.
Persamaan kuadrat lengkap :
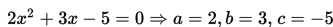
Persamaan kuadrat tidak lengkap :
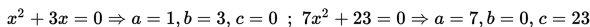
Penggunaan Diskriminan
Bentuk b2 - 4ac pada rumus kuadrat disebut diskriminan.
Diskriminan berguna untuk menentukan jenis akar-akar suatu persamaan kuadrat.
Diskriminan berguna untuk menentukan jenis akar-akar suatu persamaan kuadrat.
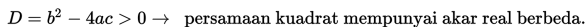


Contoh :
Tentukan jenis akar-akar persamaan kuadrat x2 - 4x + 4 = 0.
Penyelesaian :
a = 1, b = -4, dan c = 4.
a = 1, b = -4, dan c = 4.

Karena nilai diskriminan persamaan kuadrat tersebut sama dengan nol, berarti persamaan kuadrat x2 - 4x + 4 = 0 memiliki akar real sama (akar real kembar).
Mengenai pembuktiannya dengan metode pemfaktoran, dapat kalian pelajari pada topic selanjutnya tentang menentukan penyelesaian persamaan kuadrat.
Mengenai pembuktiannya dengan metode pemfaktoran, dapat kalian pelajari pada topic selanjutnya tentang menentukan penyelesaian persamaan kuadrat.
Sifat-sifat Akar Persamaan Kuadrat
Jika x1 dan x2 adalah akar-akar persamaan kuadrat ax2 + bx + c = 0 , maka akar-akar tersebut memenuhi sifat :
Jumlah akar-akarnya :
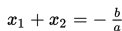
Hasil kali akar-akarnya :
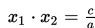
Selisih akar-akarnya :
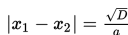
Apabila kedua akar tersebut berlainan tanda maka berlaku x1 . x2 < 0
Apabila kedua akar tesebut saling berkebalikan maka berlaku x1 . x2 = 1
Contoh :
Tentukan jumlah dan hasil kali akar-akar persamaan x2 - 4x +4 = 0 .
Penyelesaian :
a = 1, b = -4, dan c = 4.
a = 1, b = -4, dan c = 4.
Jumlah akar-akar =
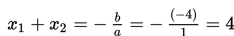
Hasil kali akar-akar =
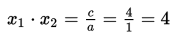
S1
Berikut ini merupakan pernyataan yang benar tentang persamaan kuadrat -3x2 + 2x - 5 = 0 adalah …
S2
Berikut ini yang merupakan persamaan kuadrat tidak lengkap adalah ….
S3
Nilai-nilai di bawah ini yang memenuhi x2 - 3x + 2 = 0 adalah …
S4
Berikut ini pernyataan yang benar tentang diskriminan suatu persamaan kuadrat adalah ….
S5
Berikut ini pernyataan yang benar tentang persamaan kuadrat x2 + 7x + 12 = 0 adalah ….
S6
Jumlah akar-akar persamaan kuadrat 2x2 + 6x - 7 = 0 adalah ….
S7
Hasil kali akar-akar persamaan 4x2 + 2x = 0 adalah ….
S8
Selisih akar-akar persamaan x2 - 11x + 30 = 0 adalah ….
S9
Misalkan x1 dan x2 adalah akar-akar dari suatu persamaan kuadrat. Jika diketahui bahwa kedua akar tersebut berlainan tanda, maka berlaku ….
S10
Misalkan x1 dan x2 adalah akar-akar dari suatu persamaan kuadrat. Jika diketahui bahwa kedua akar tersebut saling berkebalikan, maka berlaku …
