Contoh Soal Menentukan Penyelesaian Persamaan Kuadrat
Contoh Soal Menentukan Penyelesaian Persamaan Kuadrat - Menentukan penyelesaian persamaan kuadrat artinya kita harus mencari akar-akar dari persamaan kuadrat tersebut.
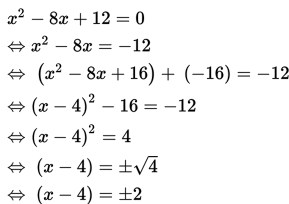
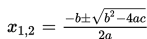
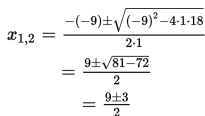
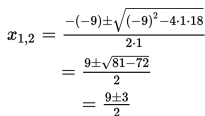
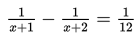
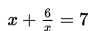
Masih ingatkah kalian apa yang dimaksud dengan akar-akar persamaan kuadrat?
Ya, akar-akar persamaan kuadrat ax2 + bx + c = 0 adalah nilai-nilai x yang memenuhi persamaan tersebut.
Ya, akar-akar persamaan kuadrat ax2 + bx + c = 0 adalah nilai-nilai x yang memenuhi persamaan tersebut.
Terdapat beberapa cara untuk menentukan akar-akar suatu persamaan kuadrat, yaitu dengan metode pemfaktoran, metode kuadrat sempurna, dan metode rumus kuadrat.
Mari kita simak satu per satu metode-metode tersebut.
Mari kita simak satu per satu metode-metode tersebut.
1) Metode Pemfaktoran
Apakah kalian masih ingat cara memfaktorkan bentuk aljabar derajat dua dengan satu variabel yang telah dibahas sebelumnya?
Cara tersebut dapat kalian gunakan untuk menentukan akar-akar suatu persamaan kuadrat seperti pada contoh berikut ini.
Cara tersebut dapat kalian gunakan untuk menentukan akar-akar suatu persamaan kuadrat seperti pada contoh berikut ini.
Contoh 1:
Tentukan akar-akar persamaan x2 - 7x + 12 = 0
Jawab :
Pemfaktoran dari x2 - 7x + 12 adalah (x - 3)(x - 4).
Sehingga,
x2 - 7x + 1 = 0
(x - 3)(x - 4) = 0
x - 3 = 0 atau x - 4 = 0
x = 3 atau x = 4
Sehingga,
x2 - 7x + 1 = 0
(x - 3)(x - 4) = 0
x - 3 = 0 atau x - 4 = 0
x = 3 atau x = 4
Jadi, akar-akar persamaan di atas adalah x1 = 3 atau x2 = 4.
Contoh 2
Tentukan akar-akar persamaan 2x2 - 5x - 3 = 0
Jawab :
Pemfaktoran dari 2x2 - 5x - 3 adalah (2x - 1)(x + 3).
Sehingga,
2x2 - 5x - 3 = 0
(2x - 1)(x + 3) = 0
2x - 1 = 0 atau x + 3 = 0
x = ½ atau x = -3
Sehingga,
2x2 - 5x - 3 = 0
(2x - 1)(x + 3) = 0
2x - 1 = 0 atau x + 3 = 0
x = ½ atau x = -3
Jadi, akar-akar persamaan di atas adalah x1 = ½ atau x2 = -3.
2) Metode Kuadrat Sempurna
Menentukan penyelesaian suatu persamaan kuadrat menggunakan metode kuadrat sempurna seringkali disebut sebagai cara kreatif.
Mengapa demikian? Karena dalam metode ini kita harus kreatif dalam menentukan bentuk kuadrat sempurna dari persamaan kuadrat yang diberikan.
Untuk lebih jelasnya, mari kita simak contoh berikut ini.
Mengapa demikian? Karena dalam metode ini kita harus kreatif dalam menentukan bentuk kuadrat sempurna dari persamaan kuadrat yang diberikan.
Untuk lebih jelasnya, mari kita simak contoh berikut ini.
Contoh:
Dengan metode kuadrat sempurna, tentukan akar-akar dari persamaan x2 - 10x + 21 = 0
Jawab :
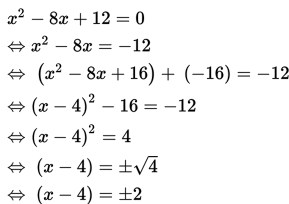
Diperoleh
x1 - 4 = 2
x1 = 6
x1 = 6
atau
x2 - 4 = -2
x2 = 2
x2 - 4 = -2
x2 = 2
Jadi, akar-akar persamaan di atas adalah x1 = 6 atau x2 = 2
3) Metode Rumus Kuadrat
Akar-akar persamaan ax2 + bx + c = 0 adalah
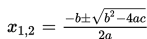
Contoh:
Dengan metode rumus kuadrat, tentukan penyelesaian persamaan x2 - 9x + 18 = 0
Jawab :
x2 – 9x + 18 = 0 → a = 1, b = -9, c = 18
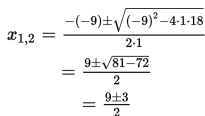
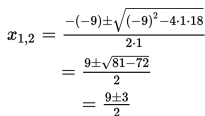
Diperoleh
x1 = (9 + 3)/2 = 6
atau
x2 = (9 - 3)/2 = 3
x1 = (9 + 3)/2 = 6
atau
x2 = (9 - 3)/2 = 3
Jadi, penyelesaian persamaan di atas adalah x1 = 6 atau x2 = 3
S1
Salah satu penyelesaian dari persamaan kuadrat x2 - 4x - 12 = 0 adalah ....
S2
Himpunan penyelesaian dari persamaan kuadrat 16x2 - 25 = 0 adalah ...
S3
Himpunan penyelesaian dari persamaan (x + 1)2 - 3(x + 2) = 7 adalah ....
S4
Dengan melengkapkan kuadrat sempurna, bentuk x2 + 8x = 9 dapat dinyatakan dalam bentuk ....
S5
Berikut ini persamaan kuadrat yang akar-akarnya 5 dan –3 adalah ....
S6
Persamaan kuadrat berikut yang akar-akarnya adalah –3 dan 7 adalah ....
S7
Hasil kali dua buah bilangan genap yang berurutan adalah 624. Bilangan genap yang kedua adalah ....
S8
Dengan menggunakan rumus kuadrat, akar-akar persamaan 2x2 + 5x + 5 = 0 adalah ....
S9
Himpunan penyelesaian dari
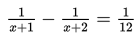
adalah ….
S10
Himpunan penyelesaian dari
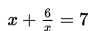
adalah ….
