Contoh Soal Menyelesaikan Persamaan Kuadrat dengan Menggunakan Grafik
Contoh Soal Menyelesaikan Persamaan Kuadrat dengan Menggunakan Grafik - Jika pada topik sebelumnya kita telah membahas tentang berbagai metode untuk menyelesaikan persamaan kuadrat, pada topik kali ini kita akan membahas cara lain untuk menyelesaikan suatu persamaan kuadrat.
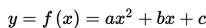
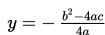
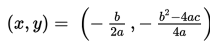
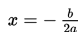
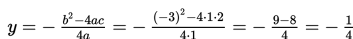
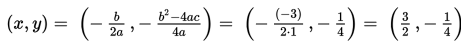
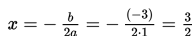
Cara lain tersebut adalah dengan menggunakan grafik.
Mau tahu caranya? Mari kita simak topik berikut ini.
1) Grafik Fungsi Kuadrat
Grafik yang digunakan untuk menyelesaikan persamaan kuadrat adalah grafik fungsi kuadrat.
Bentuk umum fungsi kuadrat adalah :
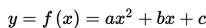
Dengan a ≠ 0 dan a, b, c bilangan real.
Grafik fungsi kuadrat berupa parabola.
Jadi sebelum membuat grafik, terlebih dahulu kita harus menentukan fungsi kuadrat yang sesuai dengan persamaan kuadrat yang hendak kita selesaikan.
Contoh:
Diberikan persamaan kuadrat x2 - 3x + 2 = 0, fungsi kuadrat yang sesuai dengan persamaan kuadrat tersebut adalah y = f(x) = x2 - 3x + 2
2) Menggambar Grafik Fungsi Kuadrat
Berikut ini adalah langkah-langkah untuk menggambar grafik fungsi kuadrat :
a) Tentukan nilai ekstrim fungsi kuadrat, yaitu:
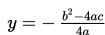
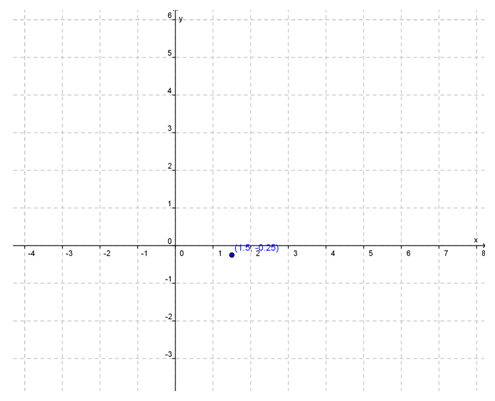
b) Tentukan titik puncak grafik, yaitu:
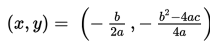
c) Tentukan sumbu simetri grafik, yaitu:
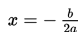
d) Tentukan titik-titik sembarang (x,y) yang memenuhi fungsi kuadrat tersebut.
e) Hubungkan titik-titik yang diperoleh sehingga terbentuk suatu kurva.
e) Hubungkan titik-titik yang diperoleh sehingga terbentuk suatu kurva.
Contoh :
Buatlah grafik fungsi kuadrat y = f(x) = x2 - 3x + 2
Jawab :
y = f(x) = x2 - 3x + 2, a = 1, b = -3, c = 2
a) Nilai ekstrim fungsi kuadrat, yaitu:
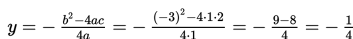
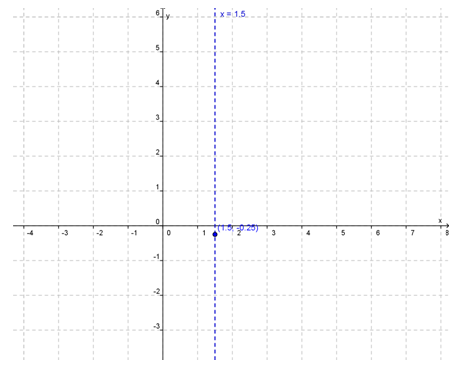
b) Titik puncak grafik, yaitu:
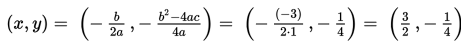

c) Sumbu simetri grafik, yaitu:
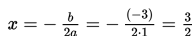

d) Titik-titiksembarang (x,y) yang memenuhifungsikuadrattersebut.
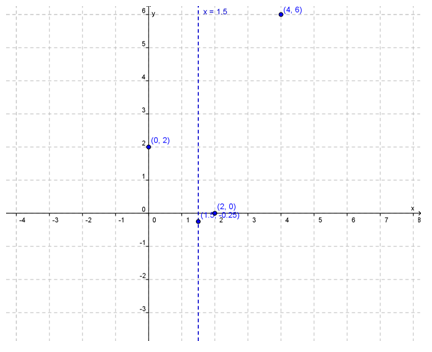
Untuk x = 0 → y = 02 – 3(0) + 2 = 2 → (0,2)
Untukx = 2 → y = 22 – 3(2) + 2 = 0 → (2,0)
Untuk x = 4 → y = 42 – 3(4) + 2 = 6 → (4,6)
Untuk x = 0 → y = 02 – 3(0) + 2 = 2 → (0,2)
Untukx = 2 → y = 22 – 3(2) + 2 = 0 → (2,0)
Untuk x = 4 → y = 42 – 3(4) + 2 = 6 → (4,6)

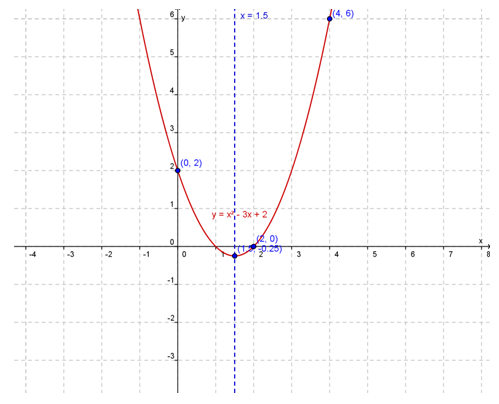
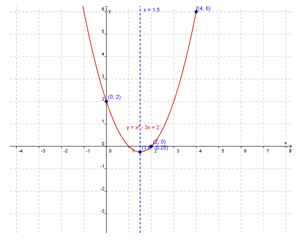
e) Hubungkan titik-titik yang diperoleh sehingga terbentuk suatu kurva.

3) Menentukan Penyelesaian Persamaan Kuadrat Menggunakan Grafik Fungsi Kuadrat
Penyelesaian persamaan kuadrat ax2 + bx + c = 0 adalah nilai absis dari titik potong kurva y = f(x) = ax2 + bx + c dengan sumbu X.
Contoh :
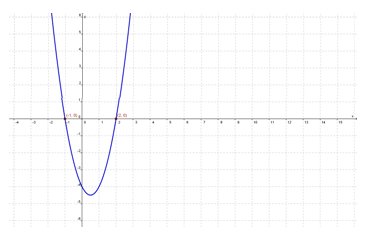
Perhatikan kurva y = f(x) = x2 - 3x + 2 berikut ini.

Titik potong kurva y = f(x) = ax2 + bx + c dengan sumbu X adalah (1,0) dan (2,0).
Dengan demikian penyelesaian dari persamaan kuadrat ax2 + bx + c = 0 adalah x = 1 atau x = 2.
S1
Grafik yang digunakan untuk menyelesaikan persamaan kuadrat adalah ....
S2
Berikut ini fungsi kuadrat yang sesuai dengan persamaan kuadrat 2x2 + 3x - 4 = 0 adalah ....
S3
Penyelesaian persamaan kuadrat ax2 + bx + c = 0 adalah ....
S4
Grafik fungsi kuadrat berupa ....
S5
Berikut ini adalah titik yang memenuhi fungsi kuadrat y = f(x) = 3x2 - 2x + 5 adalah ....
S6
Perhatikan gambar kurva berikut :

Kurva di atas merupakan kurva fungsi kuadrat ….
S7
Diberikan grafik suatu fungsi kuadrat sebagai berikut :

Berdasarkan grafik di atas, penyelesaian dari persamaan kuadrat yang bersesuaian dengan fungsi kuadrat tersebut adalah ...
S8
Grafik di bawah ini yang menunjukkan penyelesaian dari persamaan kuadrat x2 - 6x + 8 = 0 adalah ....
S9
Diberikan grafik suatu fungsi kuadrat sebagai berikut :

Berdasarkan grafik di atas, penyelesaian dari persamaan kuadrat yang bersesuaian dengan fungsi kuadrat tersebut adalah ...
S10
Perhatikan grafik berikut ini :

Berdasarkan grafik di atas, penyelesaian dari persamaan kuadrat yang bersesuaian dengan fungsi kuadrat tersebut adalah ...
