Aturan Sinus dan Cosinus Untuk Mencari Panjang
Aturan Sinus dan Cosinus Untuk Mencari Panjang -Seperti yang kamu tahu, untuk menentukan panjang suatu sisi segitiga kita dapat menggunakan dua aturan dasar sinus dan cosinus dengan merubah bentuknya sesuai kebutuhan.
Disini kamu akan mempelajari bagaimana menggunakan aturan sinus dan cosinus berdasarkan pertanyaan.
Menggunakan aturan Sinus untuk menentukan panjang suatu sisi
Ingat bahwa aturan sinus adalah perbandingan dari pasangan panjang sisi dengan sudut dihadapannya untuk menentukan salah satu yang belum diketahui dari pasangan panjang sisi dengan sudut dihadannya yang lain.
-Ketika diketahui dua sudut dan satu sisi, kamu gunakan aturan sinus dalam bentuk berikut.
a/sinA = b/sinB
kamu tidak perlu menuliskan secara lengkap rumusnya yang terdiri dari tiga perbandingan karena kamu hanya membutuhkan dua sudut dan dua sisi pada suatu waktu.
Menggunakan aturan Cosinus untuk menentukan panjang suatu sisiAturan cosinus dapat digunaka untuk menyelesaikan masalah pada semua jenis segitga Aturan ini dapat diaplikasikan untuk segitiga siku-siku dan juga segitiga sembarang.
Ingat bahwa teknik menggunakan aturan cosinus sama dengan teknik menggunakan aturan sinus. Tetapi, jika kamu akan menentukan panjang suatu sisi kamu akan menggunakan aturan cosinus dengan panjang sisi yang tidak diketahui di satu sisi dan sudut masing-masing di sisi lain dari rumus.
a2 = b2 + c2 - 2bc cos (A)
Contoh 1
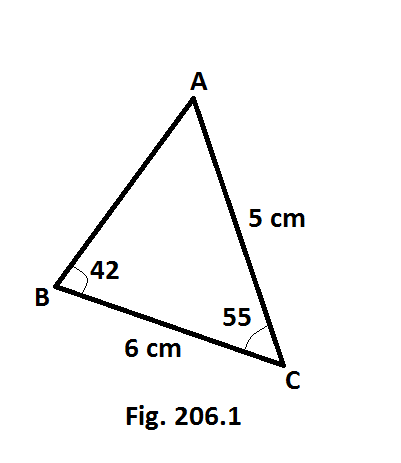
Berapa panjang AB pada segitiga berikut. Berikan jawabanmu tepat 3 angka [Gb. 206.1]
A 15.0 cm
B 6.12 cm
C 3.0 cm
D 5.0 cm
E 7.0 cm
Sekarang, gunakan aturan cosinus untuk menentukan panjang XZ:
y2 = x2 + z2 - 2xz cos (Y)
--> = 172 + 192 - 2(17)(19) [cos (13.7)]
--> = 650 - 627.62 = 22.37 ≃ 22.4 units.
Contoh 4
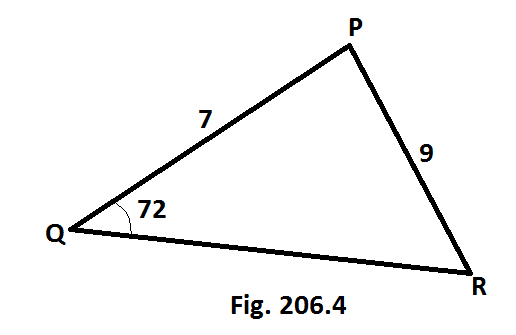
Tentukan panjang sisi yang belum diketahui dan sudut P menggunakan aturan sinus dan cosinus yang sesuai, berikan jawabanmu tepat 3 angka.[Gb.206.4]
 |
| Aturan Sinus dan Cosinus Untuk Mencari Panjang |
Disini kamu akan mempelajari bagaimana menggunakan aturan sinus dan cosinus berdasarkan pertanyaan.
Menggunakan aturan Sinus untuk menentukan panjang suatu sisi
Ingat bahwa aturan sinus adalah perbandingan dari pasangan panjang sisi dengan sudut dihadapannya untuk menentukan salah satu yang belum diketahui dari pasangan panjang sisi dengan sudut dihadannya yang lain.
-Ketika diketahui dua sudut dan satu sisi, kamu gunakan aturan sinus dalam bentuk berikut.
a/sinA = b/sinB
kamu tidak perlu menuliskan secara lengkap rumusnya yang terdiri dari tiga perbandingan karena kamu hanya membutuhkan dua sudut dan dua sisi pada suatu waktu.
Menggunakan aturan Cosinus untuk menentukan panjang suatu sisiAturan cosinus dapat digunaka untuk menyelesaikan masalah pada semua jenis segitga Aturan ini dapat diaplikasikan untuk segitiga siku-siku dan juga segitiga sembarang.
Ingat bahwa teknik menggunakan aturan cosinus sama dengan teknik menggunakan aturan sinus. Tetapi, jika kamu akan menentukan panjang suatu sisi kamu akan menggunakan aturan cosinus dengan panjang sisi yang tidak diketahui di satu sisi dan sudut masing-masing di sisi lain dari rumus.
a2 = b2 + c2 - 2bc cos (A)
Contoh 1
Berapa panjang AB pada segitiga berikut. Berikan jawabanmu tepat 3 angka [Gb. 206.1]
A 15.0 cm
B 6.12 cm
C 3.0 cm
D 5.0 cm
E 7.0 cm

Jawaban B
Penjelasan
Gunakan aturan sinus
b/sinB = c/sinC
5/sin42 = AB/sin55
AB = 6.12 cm
Contoh 2
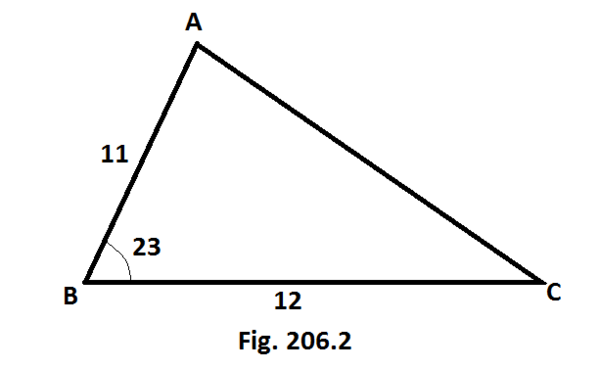
Tentukan panjang sisi yang tidak diketahui dari segitiga berikut dalam satuan meter (m) [Gb. 206.2].
A 66 m
B 22 m
C 21 m
D 16 m
E 161 m
Jawaban B
Penjelasan
Gunakan aturan sinus
b/sinB = c/sinC
5/sin42 = AB/sin55
AB = 6.12 cm
Contoh 2
Tentukan panjang sisi yang tidak diketahui dari segitiga berikut dalam satuan meter (m) [Gb. 206.2].
A 66 m
B 22 m
C 21 m
D 16 m
E 161 m
Jawaban B

Penjelasan
b2 = a2 + c2 - 2ac cos (B)
= 122 + 112 - 2(12)(11) cos (23)
= 21.98 ≃ 22
Contoh 3
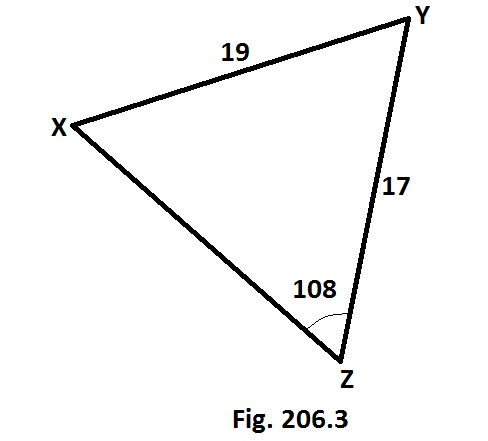
Tentukan panjang sisi yang tidak diketahui dari segitiga, dengan terlebih dahulu menentukan sudut dihadapannya. [ Gb. 206.3]. Berikan jawabanmu tepat 2 angka.
A 4.4
B 4.6
C 4.7
D 4.8
E 5.2
b2 = a2 + c2 - 2ac cos (B)
= 122 + 112 - 2(12)(11) cos (23)
= 21.98 ≃ 22
Contoh 3
Tentukan panjang sisi yang tidak diketahui dari segitiga, dengan terlebih dahulu menentukan sudut dihadapannya. [ Gb. 206.3]. Berikan jawabanmu tepat 2 angka.
A 4.4
B 4.6
C 4.7
D 4.8
E 5.2

Penjelasan
Perhatikan bahwa panjang yang tidak diketahui pada Gb. 206.3 adalah XZ tetapi sudut dihadapannya juga tidak diketahui. Sehingga, kamu perlu menentukan ∡Y terlebih dahulu.
Cara yang mudah adalah menggunakan aturan sinus:
a/sinA = b/sinB
--> z/sinZ = x/sinX
--> 19/sin108 = 17/sinX
Perhatikan bahwa panjang yang tidak diketahui pada Gb. 206.3 adalah XZ tetapi sudut dihadapannya juga tidak diketahui. Sehingga, kamu perlu menentukan ∡Y terlebih dahulu.
Cara yang mudah adalah menggunakan aturan sinus:
a/sinA = b/sinB
--> z/sinZ = x/sinX
--> 19/sin108 = 17/sinX
--> ∡ X = 58.314 ≃ 58.3
Ingat bahwa jumlah semua sudut dalam segitiga selalu 180∘. Jadi,
--> ∡ Y = 180 - 108 - 58.3 = 13.68 ≃ 13.7∘
Ingat bahwa jumlah semua sudut dalam segitiga selalu 180∘. Jadi,
--> ∡ Y = 180 - 108 - 58.3 = 13.68 ≃ 13.7∘
Sekarang, gunakan aturan cosinus untuk menentukan panjang XZ:
y2 = x2 + z2 - 2xz cos (Y)
--> = 172 + 192 - 2(17)(19) [cos (13.7)]
--> = 650 - 627.62 = 22.37 ≃ 22.4 units.
Contoh 4
Tentukan panjang sisi yang belum diketahui dan sudut P menggunakan aturan sinus dan cosinus yang sesuai, berikan jawabanmu tepat 3 angka.[Gb.206.4]

A ∡P = 60.3∘, p = 8.22
B ∡P = 60.3∘, p = 8.23
C ∡P = 60.2∘, p = 8.22
D ∡P = 60.2∘, p = 8.23
E ∡P = 60.0∘, p = 8.20
Jawaban A
Penjelasan
Menggunakan aturan sinus untuk menentukan sudut adalah cara paling mudah dalam kasus ini.
a/sinA = b/sinB
--> q/sinQ = r/sinR
--> 9/sin72 = 7/sinR
--> ∡ R = 47.7∘
Sehingga, ∡ P = 180∘ - 72∘ - 47.7∘ = 60.29∘ ≃ 60.3∘
Kita sekarang memiliki dua sisi dan satu sudut yang sesuai untuk menemukan panjang QR. Oleh sebab itu kita akan menggunakan aturan cosinus:
a2 = b2 + c2 - 2bc cos (A)
Pada kasus ini, p2 = q2 + r2 - 2qr cos (P)
--> p2 = 92 + 72 - 2(9)(7) [cos(60.3)]
--> p2 = 67.56 (Akarkan kedua sisi)
--> p = 8.219 ≃ 8.22 satuan.
B ∡P = 60.3∘, p = 8.23
C ∡P = 60.2∘, p = 8.22
D ∡P = 60.2∘, p = 8.23
E ∡P = 60.0∘, p = 8.20
Jawaban A
Penjelasan
Menggunakan aturan sinus untuk menentukan sudut adalah cara paling mudah dalam kasus ini.
a/sinA = b/sinB
--> q/sinQ = r/sinR
--> 9/sin72 = 7/sinR
--> ∡ R = 47.7∘
Sehingga, ∡ P = 180∘ - 72∘ - 47.7∘ = 60.29∘ ≃ 60.3∘
Kita sekarang memiliki dua sisi dan satu sudut yang sesuai untuk menemukan panjang QR. Oleh sebab itu kita akan menggunakan aturan cosinus:
a2 = b2 + c2 - 2bc cos (A)
Pada kasus ini, p2 = q2 + r2 - 2qr cos (P)
--> p2 = 92 + 72 - 2(9)(7) [cos(60.3)]
--> p2 = 67.56 (Akarkan kedua sisi)
--> p = 8.219 ≃ 8.22 satuan.