Penggunakan Aturan Sinus dan Aturan Cosinus
Penggunakan Aturan Sinus dan Aturan Cosinus - Pada segitiga siku-siku torema yang digunakan adalah Teorema Phytagoras.
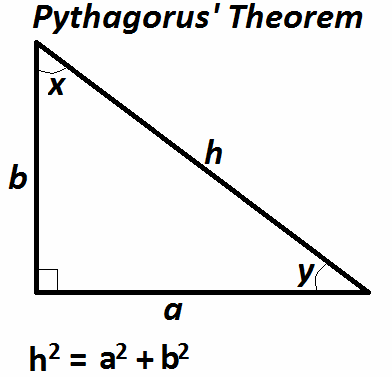
Untuk menemukan y
sinθ = siny = b/h dan,
cosθ = cosy = a/h


x + 55 + 85 = 180
x = 180 - 55 - 85
= 40
Sehingga, ∡x = 40
 |
| Penggunakan Aturan Sinus dan Aturan Cosinus |

Pada kasus sederhana, misalkan diketahui dua sisi yaitu sisi a dan sisi b seperti pada gambar di atas, untuk menentukan suatu sudut dapat digunakan rumus sinus atau cosinus.
sinθ = sisi di depan sudut/sisi miring
Misalkan a adalah sisi di depan sudut, maka θ = x
Oleh karena itu sinθ = a/h
Dan,
cosθ = sisi disamping sudut/sisi miring, maka θ = x
Oleh karena itu cosθ = b/h
Oleh karena itu sinθ = a/h
Dan,
cosθ = sisi disamping sudut/sisi miring, maka θ = x
Oleh karena itu cosθ = b/h
Untuk menemukan y
sinθ = siny = b/h dan,
cosθ = cosy = a/h

Aturan Sinus
- Aturan ini digunakan ketika diketahui panjang suatu sisi, suatu sudut dihadapan sisi tersebut serta suatu sudut yang dihadapannya terdapat sisi yang akan dicari panjangnya, atau,
- suatu sisi yang dihadapannya terdapat suatu sudut yang akan dicari besarnya.
Aturan sinus ini menggunakan perbandingan dari pasangan panjang sisi dengan sudut dihadapannya untuk menemukan salah satu bagian dari pasangan panjang sisi dan sudut lainnya.
Aturan ini dapat digunakan pada semua segitiga (tidak hanya segitiga sembarang) yang tidak memiliki sudut siku-siku.
Menentukan sisi
Jika kamu akan mencari panjang suatu sisi, kamu perlu menggunakan aturan sinus dalam bentuk berikut.
a/sinA = b/sinB
INGAT KAMU PERLU TAHU BAHWA PALING TIDAK SATU PASANG SISI DENGAN SUDUT DIHADAPANNYA UNTUK MENGGUNAKAN ATURAN SINUS.
Menentukan sudut
Jika kamu akan mencari besar suatu sudut kamu dapat menggunakan aturan sinus dalam bentuk seperti berikut.
sinA/a = sinB/b
Kamu tidak perlu menulis ketiga perbandingan sekaligus karena kamu hanya akan membutuhkan dua sudut dan dua sisi pada suatu waktu.
Menentukan sisi
Jika kamu akan mencari panjang suatu sisi, kamu perlu menggunakan aturan sinus dalam bentuk berikut.
a/sinA = b/sinB
INGAT KAMU PERLU TAHU BAHWA PALING TIDAK SATU PASANG SISI DENGAN SUDUT DIHADAPANNYA UNTUK MENGGUNAKAN ATURAN SINUS.
Menentukan sudut
Jika kamu akan mencari besar suatu sudut kamu dapat menggunakan aturan sinus dalam bentuk seperti berikut.
sinA/a = sinB/b
Kamu tidak perlu menulis ketiga perbandingan sekaligus karena kamu hanya akan membutuhkan dua sudut dan dua sisi pada suatu waktu.

Aturan Cosinus
- Aturan cosinus digunakan jika diketahui tiga panjang sisi dari suatu segitiga sembarang(bukan segitiga siku-siku) dan akan dicari besar suatu sudut, atau,
- Dapat juga digunakan untuk mencari panjang suatu sisi ketika diketahui suatu sudut dan dua sisi untuk menentukan panjang sisi yang tersisa.
Hal ini digunakan sebagai berikut
Untuk menentukan sisia2 = b2 + c2 - 2bc cos (A)Dapat juga dirubah ke dalam bentuk lain untuk menentukan sudut as
cos (A) = ( b2 + c2 -a2 )/ 2bc
Aturan cosinus digunakan pada semua kasus segitiga yang perlu menghubungkan ketiga sisi segitiga dengan satu sudut.
Jika kamu akan menentukan panjang suatu sisi, kamu membutuhkan dua sisi lainnya dan sudut dihadapannya.
Contoh 1
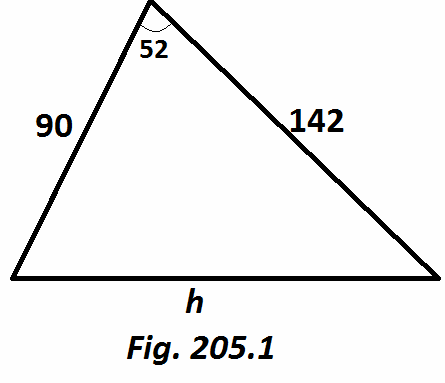
Tentukan sisi yang belum dikatahui dari segitiga pada [Gb. 205.1] di bawah ini.
A 111
B 110
C 630
D 6390
E 112
Jawaban E
B 110
C 630
D 6390
E 112
Jawaban E
Penjelasan
a2 = b2 + c2 - 2bc cos (A)
h2 = 902 + 1422 - 2(90)(142)cos(52)
= 28264 - 15736.30
= 12527 (Akarkan kedua sisi)
h = 111.9
a2 = b2 + c2 - 2bc cos (A)
h2 = 902 + 1422 - 2(90)(142)cos(52)
= 28264 - 15736.30
= 12527 (Akarkan kedua sisi)
h = 111.9
≃ 112
Contoh 2
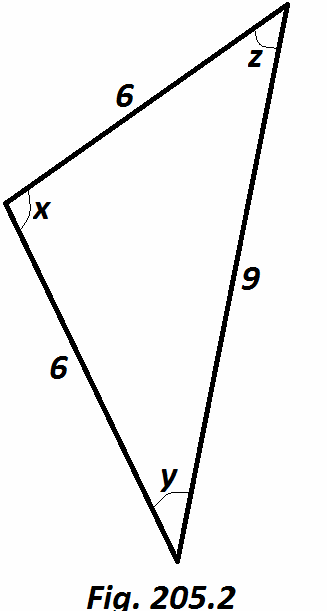
Tentukan besar sudut x, y dan z dari segitiga berikut dengan tepat satu angka dibelakang koma.
[Gb. 205.2]
Contoh 2
Tentukan besar sudut x, y dan z dari segitiga berikut dengan tepat satu angka dibelakang koma.
[Gb. 205.2]

A x=98.2, y=70.1, z=11.7
B x=82.8, y=41.4, z=41.4
C x=97.2, y=41.4, z=41.4
D x= 82.8, y=44, z=53.2
E x=126.8, y=26.6, z=26.6
Jawaban C
Penjelasan
Gunakan aturan cosinus
a2 = b2 + c2 - 2bc cos (A)
x2 = y2 + z2 – 2yz cos (X)
B x=82.8, y=41.4, z=41.4
C x=97.2, y=41.4, z=41.4
D x= 82.8, y=44, z=53.2
E x=126.8, y=26.6, z=26.6
Jawaban C
Penjelasan
Gunakan aturan cosinus
a2 = b2 + c2 - 2bc cos (A)
x2 = y2 + z2 – 2yz cos (X)
(y2 + z2 - x2 )/2yz =
cosx
Contoh 3
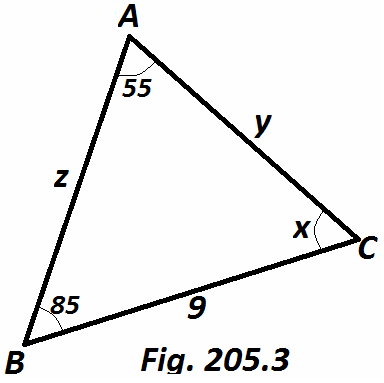
Tentukan nilai dari x, y dan z dari segitiga pada Gb. 205.3
A x=11, y=11, z=8.6
B x=40, y=11, z=8.6
C x=50, y=11, z= 8.6
D x=40, y=10, z= 9.0
E x=40, y=10, z= 9.0
Jawaban B
cosx
(62 + 62 - 92 )/2(6)(6) = cosx
(72-81)/72 = cosx
- 9/72 = cosx
- 1/8 = cosx
x = 97.1807 ≃ 97.2
Sekarang gunakan aturan sinus
(72-81)/72 = cosx
- 9/72 = cosx
- 1/8 = cosx
x = 97.1807 ≃ 97.2
Sekarang gunakan aturan sinus
sinA/a = sinB/b = sinC/c
-> sinX/x = sinY/y = sinZ/z
-> sinX/9 = sinY/6 = sinZ/6
Ingat bahwa aturan sinus menggunakan perbandingan maka kamu akan menentukan y dan z dalam dua langkah sebagai berikut
-> sinX/9 = sinY/6
-> sin97.2/ = sinY/6
-> Y = 41.407 ≃ 41.4
Ingat bahwa jumlah semua sudut dalam segitiga adalah 180 derajat.
So x + y + z = 180
thus, z = 180 - x - y
z = 180 - 97.2 - 41.4
z = 41.4
-> sinX/x = sinY/y = sinZ/z
-> sinX/9 = sinY/6 = sinZ/6
Ingat bahwa aturan sinus menggunakan perbandingan maka kamu akan menentukan y dan z dalam dua langkah sebagai berikut
-> sinX/9 = sinY/6
-> sin97.2/ = sinY/6
-> Y = 41.407 ≃ 41.4
Ingat bahwa jumlah semua sudut dalam segitiga adalah 180 derajat.
So x + y + z = 180
thus, z = 180 - x - y
z = 180 - 97.2 - 41.4
z = 41.4
Contoh 3
Tentukan nilai dari x, y dan z dari segitiga pada Gb. 205.3
A x=11, y=11, z=8.6
B x=40, y=11, z=8.6
C x=50, y=11, z= 8.6
D x=40, y=10, z= 9.0
E x=40, y=10, z= 9.0

Penjelasan
Karena jumlah semua sudut dalan segitiga adalah 180
Karena jumlah semua sudut dalan segitiga adalah 180
x + 55 + 85 = 180
x = 180 - 55 - 85
Sehingga, ∡x = 40
Sekarang gunakan aturan sinus
y/sin85 = 9/sin55
y = 10.945 ≃ 11 satuan
Terakhir, karena telah diketahui dua panjang sisi segitiga dan satu sudut maka gunakan aturan cosinus untuk menentukan panjang z.
a2 = b2 + c2 - 2bc cos (A)
z2 = 112 + 92 – 2(11)(9) (cos (40)
= 74.73 (Akarkan kedua sisi)
= 8.644 ≃ 8.6
y = 10.945 ≃ 11 satuan
Terakhir, karena telah diketahui dua panjang sisi segitiga dan satu sudut maka gunakan aturan cosinus untuk menentukan panjang z.
a2 = b2 + c2 - 2bc cos (A)
z2 = 112 + 92 – 2(11)(9) (cos (40)
= 74.73 (Akarkan kedua sisi)
= 8.644 ≃ 8.6
