Contoh Soal Perbandingan Panjang Sisi-Sisi Segitiga Siku-Siku Khusus

Contoh Soal Perbandingan Panjang Sisi-Sisi Segitiga Siku-Siku Khusus - Pernahkah kalian bermain catur bersama teman atau mengikuti kejuaran catur? Permainan ini sangat identik dengan strategi dan olah pikiran. Pada permainan catur terdapat beberapa jenis biji catur (bidak), antara lain pion, raja, menteri, benteng, kuda, dan peluncur. Bidak ini digerakkan dengan aturan tertentu yang digunakan untuk melawan bidak lawan.

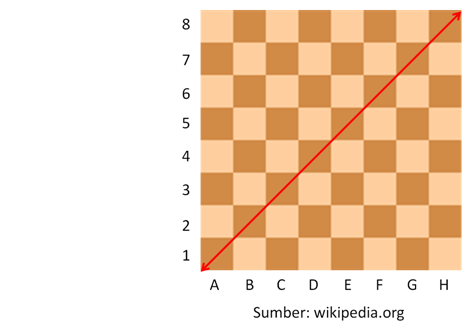
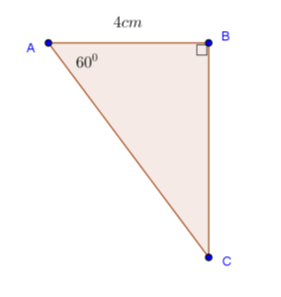
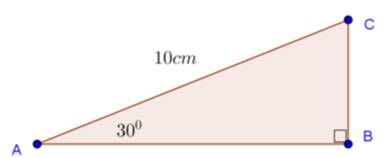
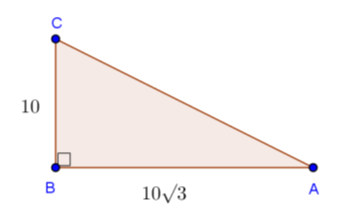
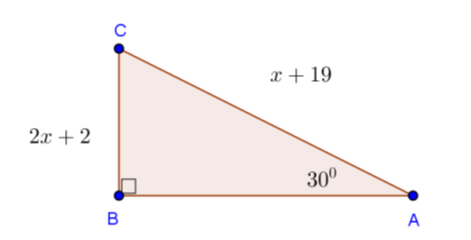
        Pada topik ini kita tidak akan mempelajari permainan catur, tapi kita akan mengunakan papan catur untuk mempermudah kalian memahami topik matematika tentang keistimewaan sisi-sisi pada segitiga siku-siku.

Misalkan kita tarik garis lurus pada papan catur dari titik sudut pada kotak A1 sampai H8. Anggaplah setiap kotak pada papan catur merupakan 1 satuan luas. Sekarang, dapatkah kita menghitung panjang ruas garis tersebut? Tentu saja bisa, salah satu caranya adalah dengan menggunakan rumus Pythagoras. 
Misalkan panjang ruas garis tersebut = d. Oleh karena papan catur berbentuk persegi, maka ruas garis tadi membagi papan catur menjadi 2 buah segitiga siku-siku yang sama besar dan ruas garis tersebut menjadi sisi miringnya.

Oleh karena itu, berlaku teorema pythagoras yaitu,

$$$\begin{array}{rll}{d}^2& =& 8^2+8^2\\ d^2& =& 2\times 8^2\\ d& =& 8\sqrt{2}\end{array}$

Jadi, panjang ruas garis tersebut = $8\sqrt{2}$ satuan.

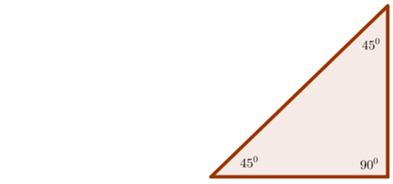
Sebenarnya kita dapat mengetahui panjang sisi miring pada segitiga siku-siku tersebut tanpa menggunakan rumus Pythagoras. Hal ini disebabkan karena segitiga siku-siku di atas mempunyai sudut-sudut yang istimewa, yaitu ${90}^{\circ }$ dan ${45}^{\circ }$. Ada beberapa sudut istimewa lain yang dapat dimiliki oleh segitiga siku-siku, yaitu sudut ${30}^{\circ }$ dan ${60}^{\circ }$. Segitiga siku-siku yang mempunyai sudut istimewa inilah yang disebut dengan Segitiga Siku-Siku Khusus.

Sisi pada segiiga siku-siku khusus memiliki keistimewaan, sehingga kita dapat menentukan panjang salah satu sisinya dengan menggunakan perbandingan tertentu. Tentu kamu penasaran bagaimana caranya bukan? Oleh karena itu, perhatikanlah materi berikut ini dengan saksama.

✾✾✾ Sudut ${30}^{\circ }$ dan ${60}^{\circ }$✾✾✾

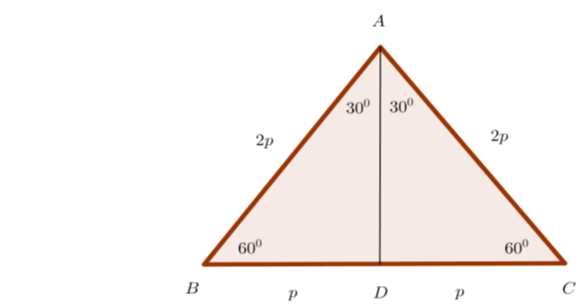
Perhatikan segitiga sama sisi ABC berikut.

Garis AD adalah garis tinggi, garis bagi, dan sekaligus garis berat dari segitiga ABC, sehingga AD membagi sisi BC sama besar.

Oleh karena AD merupakan garis tinggi pada segitiga ABC, maka segitiga ADC merupakan segitiga siku-siku di D. Oleh karena itu, berlaku teorema Pythagoras yaitu,

$\begin{array}{lcl}& A{D}^2+C{D}^2& =A{C}^2\\ \iff & A{D}^2+p^2& =(2p{)}^2\\ \iff & A{D}^2& =4p^2-2p\\ \iff & A{D}^2& =3p^2\\ \iff & AD& =p\sqrt{3}\end{array}$

Perhatikan bahwa $CD:AD:AC=p:p\sqrt{3}:2p$ atau $CD:AD:AC=1:\sqrt{3}:2$

Oleh karena,

CD adalah sisi di depan sudut ${30}^{\circ }$ 
AD adalah sisi di depan sudut ${60}^{\circ }$
AC adalah sisi di depan sudut ${90}^{\circ }$

maka kita dapatkan perbandingan berikut.

Perbandingan ini dapat digunakan untuk menyelesaikan soal segitiga siku-siku dengan sudut ${30}^{\circ }$ dan ${60}^{\circ }$ tanpa menggunakan teorema Pythagoras.

♯ ♬ Contoh Soal ♬ ♯

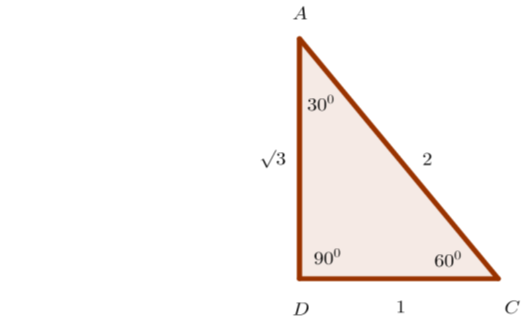
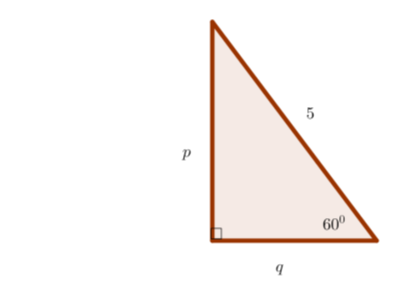
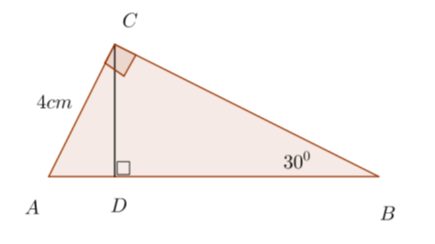
Perhatikan segitiga siku-siku di bawah ini.

Nilai p dan q pada segitiga siku-siku tersebut adalah....

Penyelesaian:

Diketahui segitiga siku-siku salah satu sudutnya adalah ${60}^{\circ }$. Oleh karena jumlah sudut pada sebuah segitiga = ${180}^{\circ }$, maka besar sudut ketiga = ${180}^{\circ }-({90}^{\circ }+{60}^{\circ })={30}^{\circ }$.

Misalkan sisi miring =r, maka pada segitiga ini berlaku,

$\begin{array}{ccccccccccc}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{30}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{60}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}& =& 1& :& \sqrt{3}& :& 2\\ q& :& p& :& r& =& 1& :& \sqrt{3}& :& 2\end{array}$.

Selanjutnya diperoleh q : r = 1 : 2 dan p : r = $3$ : 2

$\begin{array}{llll}& \frac{q}{r}& =& \frac{1}{2}\\ \iff & \frac{q}{5}& =& \frac{1}{2}\\ \iff & q& =& \frac{5\times 1}{2}\\ \iff & q& =& \frac{5}{2}\\ \iff & q& =& 2,5\end{array}$

$$

$\begin{array}{llll}& \frac{p}{r}& =& \frac{\sqrt{3}}{2}\\ \iff & \frac{p}{5}& =& \frac{\sqrt{3}}{2}\\ \iff & p& =& \frac{5\times \sqrt{3}}{2}\\ \iff & p& =& \frac{5\sqrt{3}}{2}\\ \iff & p& =& 2,5\sqrt{3}\end{array}$

Jadi, nilai $p=2,5\sqrt{3}$ dan $q=2,5$.

Trik SUPER (SOLUSI UNGGULAN QUIPPER)

Untuk mempermudah kita dalam menentukan sisi yang tidak diketahui pada segitiga siku-siku khusus, kita dapat menggunakan trik sebagai berikut.

Sisi yang telah diketahui panjangnya adalah r = 5. Nilai perbandingan r pada segitiga tersebut adalah 2. Untuk memperoleh r = 5, maka 2 harus dikalikan dengan 2,5. Jadi untuk mendapatkan panjang sisi lainnya, nilai perbandingannya harus sama-sama dikalikan dengan 2,5. Untuk lebih jelasnya perhatikan tabel berikut.

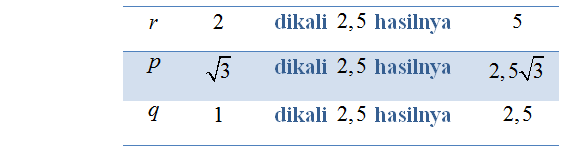
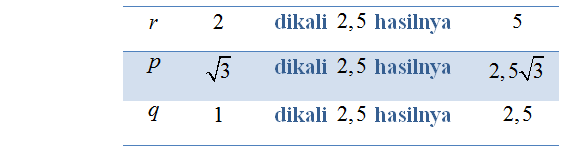
✾✾✾ Sudut ${45}^{\circ }$ ✾✾✾

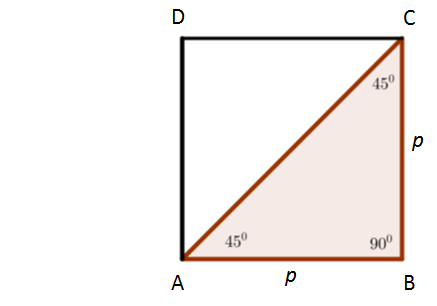
Perhatikan persegi ABCD di bawah ini.

Perhatikan bahwa ABC merupakan segitiga siku-siku sehingga berlaku teorema Pythagoras yaitu,

$\begin{array}{lcl}& A{B}^2+B{C}^2& =A{C}^2\\ \iff & p^2+p^2& =A{C}^2\\ \iff & A{C}^2& =2p^2\\ \iff & AC& =p\sqrt{2}\end{array}$

Perhatikan bahwa $AB:BC:AC=p:p:p\sqrt{2}$ atau $AB:BC:AC=1:1:\sqrt{2}$

Oleh karena,

AB adalah sisi di depan sudut ${45}^{\circ }$ 
BC adalah sisi di depan sudut ${45}^{\circ }$
AC adalah sisi di depan sudut ${90}^{\circ }$

maka kita dapatkan perbandingan berikut.

Perbandingan ini dapat digunakan untuk menyelesaikan soal segitiga siku-siku dengan sudut ${45}^{\circ }$ tanpa menggunakan rumus Pythagoras.

♯ ♬ Contoh Soal ♬ ♯

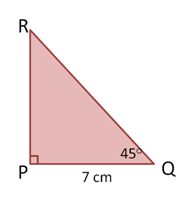
Diketahui segitiga PQR siku-siku di P dan besar sudut Q adalah ${45}^{\circ }$. Jika panjang PQ = 7 cm, maka panjang PR dan QR adalah....

Penyelesaian:

Diketahui segitiga PQR siku-siku di P, besar sudut Q = ${45}^{\circ }$, dan panjang PQ = 7 cm.

Oleh karena jumlah sudut pada sebuah segitiga = ${180}^{\circ }$, maka besar sudut R = ${180}^{\circ }-({90}^{\circ }+{45}^{\circ })={45}^{\circ }$

Oleh karena segitiga PQR adalah segitiga siku-siku khusus dengan sudut ${45}^{\circ }$, maka berlaku:

$\begin{array}{ccccccccccc}\mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{45}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{d}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{n}\mathrm{s}\mathrm{u}\mathrm{d}\mathrm{u}\mathrm{t}{45}^{\circ }& :& \mathrm{s}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{r}\mathrm{i}\mathrm{n}\mathrm{g}& =& 1& :& 1& :& \sqrt{2}\\ PQ& :& PR& :& QR& =& 1& :& 1& :& \sqrt{2}\end{array}$.

Selanjutnya diperoleh PQ : PR = 1 : 1 dan PQ : QR = 1 : $2$.

$\begin{array}{llll}& \frac{PQ}{PR}& =& \frac{1}{1}\\ \iff & \frac{7}{PR}& =& \frac{1}{1}\\ \iff & PR& =& 7\times 1\\ \iff & PR& =& 7\end{array}$

$$

$\begin{array}{llll}& \frac{PQ}{QR}& =& \frac{1}{\sqrt{2}}\\ \iff & \frac{7}{QR}& =& \frac{1}{\sqrt{2}}\\ \iff & QR& =& 7\times \sqrt{2}\\ \iff & QR& =& 7\sqrt{2}\end{array}$

Jadi, panjang PR = $7$ dan QR = $7\sqrt{2}$.

Trik SUPER (SOLUSI UNGGULAN QUIPPER)

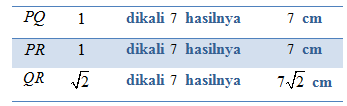
Sisi yang telah diketahui panjangnya adalah PR = 7. Nilai perbandingan PR pada segitiga tersebut adalah 1. Untuk memperoleh PR = 7, maka 1 harus dikalikan dengan 7. Jadi untuk mendapatkan panjang sisi lainnya, nilai perbandingannya harus sama-sama dikalikan dengan 7. Untuk lebih jelasnya perhatikan tabel berikut.

S1

Pilihan Tunggal

Perhatikan segitiga siku-siku di bawah ini.

Panjang sisi AC adalah ... cm

S2

Pilihan Tunggal

Perhatikah segitiga siku-siku di bawah ini.

Panjang sisi AB adalah ....

S3

Pilihan Tunggal

Diketahui $\mathrm{△}KLM$ siku-siku di M dan $\mathrm{\angle }K=\mathrm{\angle }L$. Jika panjang LK = $3\sqrt{2}$ cm maka panjang LM adalah....

S4

Pilihan Tunggal

Panjang sisi persegi ABCD adalah 6 cm. Jika AC dan BD adalah diagonal bidang persegi, maka panjang BD adalah....

S5

Pilihan Tunggal

Besar sudut C pada segitiga siku-siku di bawah ini adalah....

S6

Pilihan Tunggal

Perhatikan segitiga siku-siku di bawah ini.

Nilai x adalah....

S7

Pilihan Tunggal

Panjang sisi CD adalah....

S8

Pilihan Tunggal

Diberikan segitiga ABC siku-siku di B. Panjang AC = 8 cm dan AB = BC = p cm. Nilai $p^2$ adalah....

S9

Pilihan Tunggal

Luas persegipanjang ABCD di bawah ini adalah....

S10

Pilihan Tunggal

Luas jajargenjang ABCD di bawah ini adalah....

Share this post