Aturan dan Sifat Turunan Fungsi Aljabar
Aturan dan Sifat Turunan Fungsi Aljabar - Pada topik sebelumnya kalian telah mempelajari limit fungsi. Topik kali ini merupakan kelanjutan dari topik limit fungsi yaitu turunan. Pada topik ini kalian akan mempelajari definisi dan aturan-aturan pada turunan fungsi aljabar maupun fungsi trigonometri.
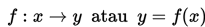
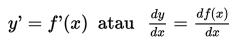
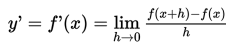
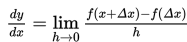
Untuk lebih jelasnya silakan simak contoh-contoh berikut.
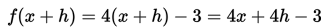
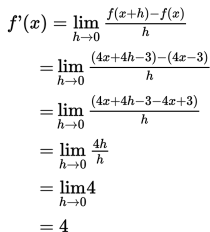
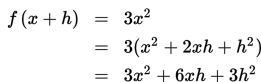
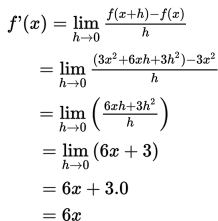
Turunan f(x) = axn adalah
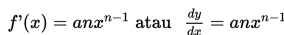
Untuk suatu fungsi u dan v, bilangan real c, dan bilangan rasional n, berlaku :
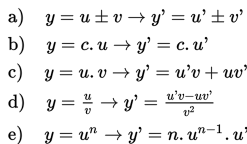
Untuk lebih jelasnya, kalian bisa mencermati contoh berikut.
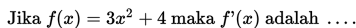
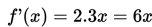
Contoh 2:
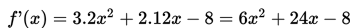
Contoh 3:
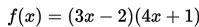

Contoh 4:
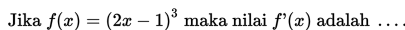
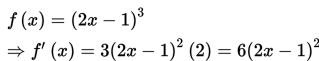
Contoh 5:
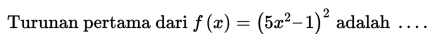
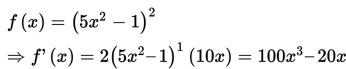
Contoh 6:

Contoh 7:

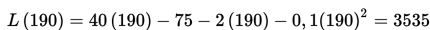
Dengan demikian, laba maksimumnya adalah Rp 3.535,00.
 |
| Aturan dan Sifat Turunan Fungsi Aljabar |
Definisi turunan:
Fungsi
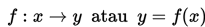
mempunyai turunan yang dinotasikan
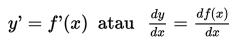
dan didefinisikan:
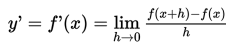
atau
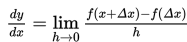
Notasi kedua ini disebut notasi Leibniz.
Untuk lebih jelasnya silakan simak contoh-contoh berikut.
Contoh 1:
Tentukan turunan dari f(x) = 4x - 3 .
Jawab:
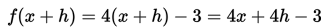
Sehingga:
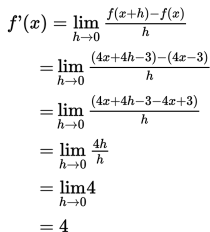
Contoh 2:
Tentukan turunan dari f(x) = 3x2.
Jawab:
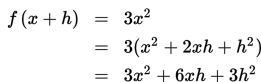
Sehingga:
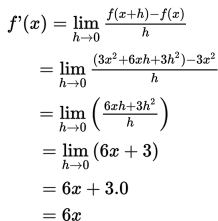
RUMUS-RUMUS TURUNAN
Setelah mempelajari definisi turunan, kalian akan mempelajari rumus-rumus turunan.
Turunan f(x) = axn adalah
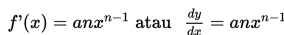
Untuk suatu fungsi u dan v, bilangan real c, dan bilangan rasional n, berlaku :
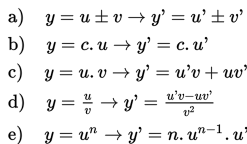
Untuk lebih jelasnya, kalian bisa mencermati contoh berikut.
Contoh 1:
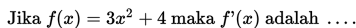
Pembahasan:
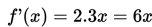
Contoh 2:
Nilai Turunan pertama dari f(x) = 2x3 + 12x2 - 8x + 4 adalah
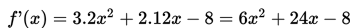
Contoh 3:
Turunan ke- 1 dari
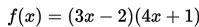
adalah ….
Pembahasan:

Contoh 4:
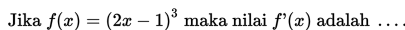
Pembahasan:
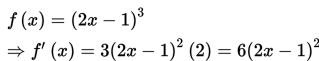
Contoh 5:
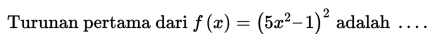
Pembahasan:
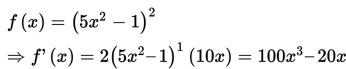
Contoh 6:
Rusuk suatu kubus bertambah panjang dengan laju 7 cm per detik.
Hitunglah laju bertambahnya volume pada saat panjang rusuknya 15 cm.
Hitunglah laju bertambahnya volume pada saat panjang rusuknya 15 cm.
Pembahasan:
Misal panjang rusuk = x cm
Setelah t detik, panjang rusuk = (x + 7t ) cm maka volume kubus setelah t detik adalah:
Setelah t detik, panjang rusuk = (x + 7t ) cm maka volume kubus setelah t detik adalah:

Contoh 7:
Suatu perusahaan menghasilkan x produk dengan biaya total sebesar 75 + 2x + 0,1x2rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp 40,00 untuk setiap produknya, maka laba maksimum yang diperoleh adalah ….
Pembahasan:
Biaya untuk x produk sebesar 75 + 2x + 0,1x2 (rupiah)
harga 1 produk = Rp 40,00
Laba maksimal bila L' = 0
harga 1 produk = Rp 40,00
Laba maksimal bila L' = 0

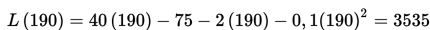
Dengan demikian, laba maksimumnya adalah Rp 3.535,00.