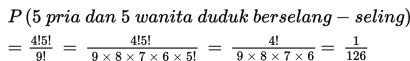Permutasi dan Kombinasi dalam Menghitung Probabilitas
Permutasi dan Kombinasi dalam Menghitung Probabilitas - Pada pelajaran sebelumnya, kalian telah belajar mengenai permutasi dan kombinasi. Akan tetapi, apakah kalian tahu tentang banyak cara menyusun sejumlah obyek jika disusun secara melingkar? Apakah konsep umum dari permutasi dan kombinasi akan digunakan?
 |
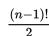
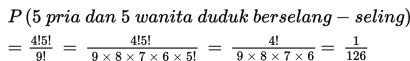
| Permutasi dan Kombinasi dalam Menghitung Probabilitas |
Dalam pelajaran ini, kalian akan belajar tentang bagaimana cara :
- Menggunakan permutasi dan kombinasi dalam menghitung probabilitas kejadian campuran.
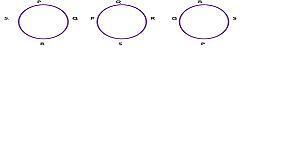
Namun sebelum itu, kita akan belajar tentang permutasi siklis terlebih dahulu, dimana sejumlah obyek disusun secara melingkar. Contoh : Terdapat 4 orang bernama P,Q, R, dan S. Mereka duduk mengelilingi sebuah meja bundar.
Jika kita menggeser posisi duduk dari P, Q, R, dan S dalam arah yang berlawanan dengan arah jarum jam, maka akan diperoleh posisi duduk sebagai berikut :
Akan tetapi, posisi duduk keempat orang ini akan terlihat sama jika kita melihat barisan PQRS dalam arah yang searah jarum jam (Q ada di kanan P, R ada di kanan Q, S ada di kanan R, dan P ada di kanan S).
Oleh karena itu, dalam penyusunan n obyek dalam posisi melingkar, kita harus menetapkan posisi dari 1 obyek terlebih dahulu, setelah itu kita baru akan mengatur (n-1) obyek sisanya dalam (n-1)! cara.
Dengan demikian, rumus untuk menyusun n obyek dalam posisi melingkar, dimana penyusunan searah jarum jam berbeda dengan penyusunan yang berlawanan arah dengan arah jarum jam adalah : (n-1)!.
Akan tetapi, jika penyusunan searah jarum jam sama dengan penyusunan yang berlawanan arah dengan arah jarum jam, maka banyak penyusunan n obyek dalam posisi melingkar adalah :
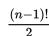
Hal ini terjadi karena hasil penyusunan dari kedua arah adalah sama dan kita akan mengulang penyusunan yang sama sebanyak dua kali. Oleh karena itulah, kita harus membagi banyak cara pengaturan dengan 2. Lebih lanjut, penyusunan manik-manik dalam kalung memberikan hasil penyusunan yang sama dalam kedua arah.
Contoh :
Dalam sebuah meja bundar, terdapat 5 orang pria dan 5 orang wanita. Berapakah probabilitas mereka duduk secara beselang-seling?
Penjelasan :
Karena kita harus menyusun pria dan wanita dalam meja bundar, maka kita akan menggunakan konsep permutasi siklis.
Adapun banyak cara menyusun posisi kelima pria dalam meja bundar adalah (n-1)! = (5-1)! = 4!.
Selanjutnya, karena ada 5 tempat duduk kosong diantara tempat duduk yang telah ditempati para pria, maka kita dapat menempatkan wanita pertama dalam 5 cara, wanita kedua dalam 4 cara, dst.
Dengan kata lain, terdapat 5 × 4 × 3 × 2 × 1 = 5! cara dalam menyusun posisi duduk wanita.
Dengan demikian, kita dapat menyusun 5 pria dan 5 wanita dalam 4!(5!) cara.
Selanjutnya, probabilitas 5 pria dan 5 wanita duduk berselang-seling adalah :
Karena banyak cara menyusun pria dan wanita dalam meja bundar adalah ((5+5)-1)! = (10-1)! = 9!, maka