Fungsi Naik dan Fungsi Turun
Fungsi Naik dan Fungsi Turun - Apakah kalian masih ingat dengan aturan dan sifat fungsi aljabar yang telah kalian pelajari pada topik sebelumnya?
Contoh 1:
Contoh 2:
Contoh 3:

 |
| Fungsi Naik dan Fungsi Turun |
Tentu masih ingat bukan? Nah, topik tersebut akan kita gunakan sebagai dasar dalam mempelajari topik kali ini. Dalam topik kali ini, kalian akan belajar mengenai fungsi naik dan fungsi turun.
Apa itu fungsi naik dan fungsi turun?
Mari kita temukan jawabannya dalam topik ini.
Mari kita temukan jawabannya dalam topik ini.
FUNGSI NAIK DAN FUNGSI TURUN
Misalkan fungsi f terdefinisi pada selang I.
- Fungsi f dikatakan monoton naik pada selang I jika untuk setiap selang (a , b)dalam I, dimana a < b maka f(a) < f(b).
- Fungsi f dikatakan monoton turun pada selang I jika untuk setiap selang (a , b)dalam I, dimana a < b maka f(a) > f(b).
Dengan kata lain,
- Jika f'(x) > 0 untuk setiap x dalam selang (a , b), maka fungsi f naik pada selang (a , b).
- Jika f'(x) < 0 untuk setiap x dalam selang (a , b), maka fungsi f turun pada selang (a, b).
CONTOH
Apakah kalian sudah paham dengan penjelasan di atas?
Agar kalian lebih paham, mari kita cermati beberapa contoh soal berikut ini.
Agar kalian lebih paham, mari kita cermati beberapa contoh soal berikut ini.
Contoh 1:
Periksa naik atau turunnya f(x) = -x2 pada selang (0 , 1).
Penyelesaian:
Turunan pertama dari f(x) = -x2 adalah f'(x) = -2x.
Jika dimisalkan p terletak pada selang (0 , 1), maka 0 < p < 1.
Dengan demikian, f'(p) = -2p < 0.
Jadi, dapat disimpulkan bahwa f(x) = -x2 pada selang (0 , 1) merupakan fungsi turun.
Contoh 2:
Periksa naik atau turunnya f(x) = 10x -x2 pada selang (0 , 10).
Penyelesaian:
Turunan pertama dari f(x) =10x -x2 adalah f'(x) = 10 - 2x.
Jika dimisalkan p terletak pada selang (0 , 10), maka 0 < p < 10.
Dengan demikian,
- f'(p) = 10 - 2p > 0 untuk 0 < p < 5
- f'(p) = 10 - 2p < 0 untuk 5 < p < 10
Jadi, dapat disimpulkan bahwa f(x) = 10x - x2 pada selang (0 , 10) merupakan fungsi naik dan fungsi turun.
Contoh 3:
Diketahui f(x) = x3 + 9x2 + 15x + 4.
Kapan fungsi f naik?
Kapan fungsi f naik?
Penyelesaian:
Turunan pertama dari f(x) = x3 + 9x2 + 15x + 4 adalah f'(x) = 3x2 + 18x + 15.
Oleh karena f(x) naik jika f'(x) > 0, maka


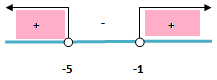
Dengan demikian, dapat disimpulkan bahwa f(x) = x3 + 9x2 + 15x + 4 naik pada interval x< - 5 atau x > 1.