Tafsiran Geometris Suatu Turunan Gradien Garis Singgung Kurva
Tafsiran Geometris Suatu Turunan Gradien Garis Singgung Kurva - Masih ingat dengan materi fungsi naik dan fungsi turun? Setelah mempelajari fungsi naik dan turun pada topik sebelumnya, pada topik ini kalian akan mengetahui salah satu penggunaan turunan, yaitu menentukan gradien garis singgung sebuah kurva.
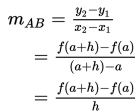
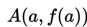
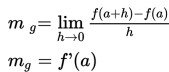
Sehingga persamaan garis singgung pada kurva y=f(x) di titik
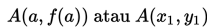
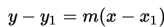
Apakah kalian sudah memahami penjelasan di atas? Jika belum terlalu jelas, kalian dapat mencermati contoh-contoh di bawah ini.
Contoh 1:
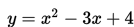
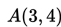
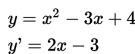
a. Gradien di titik A(3,4)
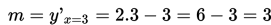
b. Persamaan garis singgung di titik A(3,4)
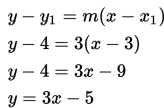
Contoh 2:
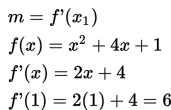
Contoh 3:
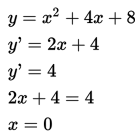
 |
| Tafsiran Geometris Suatu Turunan Gradien Garis Singgung Kurva |
Gradien garis singgung
Gradien merupakan kemiringan suatu garis lurus. Untuk menentukan gradien sebuah garis tidaklah susah. Namun, untuk menentukan gradien suatu garis singgung pada kurva lengkung membutuhkan turunan. Nah, cara menentukan gradien garis singgung sebuah kurva akan kalian pelajari pada topik ini.

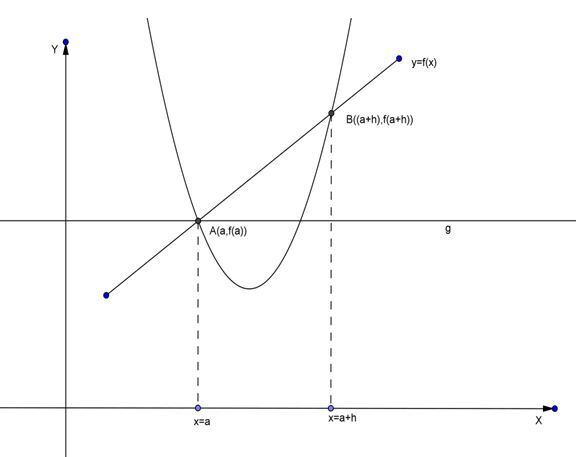
Perhatikan gambar di atas! Gradien garis AB adalah
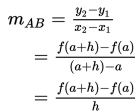
Apabila garis AB diputar pada titik A maka titik B akan bergerak mendekati titik A(h→0) maka tali busur AB menjadi garis singgung (g) pada kurva y = f(x) di titik
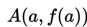
dengan gradien
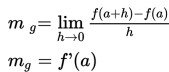
Sehingga persamaan garis singgung pada kurva y=f(x) di titik
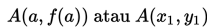
adalah
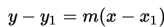
Apakah kalian sudah memahami penjelasan di atas? Jika belum terlalu jelas, kalian dapat mencermati contoh-contoh di bawah ini.
Contoh 1:
Diketahui kurva
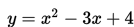
dan titik
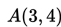
a. Tentukan gradien garis singgung di titik A.
b. Tentukan persamaan garis singgung di titik A.
b. Tentukan persamaan garis singgung di titik A.
Pembahasan:
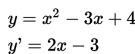
a. Gradien di titik A(3,4)
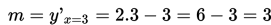
b. Persamaan garis singgung di titik A(3,4)
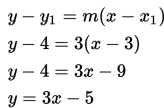
Contoh 2:
Tentukan gradien garis singgung pada kurva y =x2 + 4x + 1 di titik (1, 10).
Pembahasan:
Langkah pertama kita tentukan dulu turunan fungsi y.
Kemudian substitusikan titik ke dalam fungsi turunan pertama
Kemudian substitusikan titik ke dalam fungsi turunan pertama
- Titik singgung (1, 10)
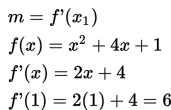
Jadi, gradien garis singgungnya adalah 6
Contoh 3:
Tentukan absis titik singgung sehingga garis singgung pada kurva y = x2 + 4x + 8 mempunyai gradien 4.
Pembahasan:
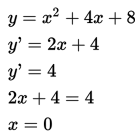
Jadi, absis titik singgung adalah 0.