Tafsiran Geometris Suatu Turunan Garis Tangen
Tafsiran Geometris Suatu Turunan Garis Tangen - Pada topik sebelumnya kalian telah belajar mengenai gradien garis singgung. Topik tersebut akan sangat berguna untuk mempelajari topik kali ini. Nah, pada topik ini, kalian akan belajar tentang bagaimana menemukan persamaan garis singgung sebuah kurva (garis tangen) di suatu titik pada kurva.
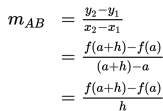
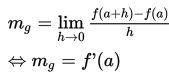
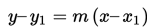
Agar kalian lebih mudah dalam memahami tafsiran geometris suatu turunan garis tangen, mari kita cermati beberapa contoh berikut ini.
Contoh 1 :
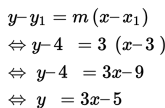
Contoh 2 :
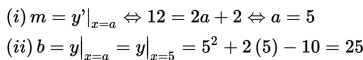
Contoh 3 :
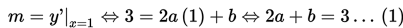
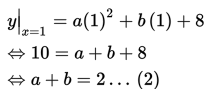
 |
| Tafsiran Geometris Suatu Turunan Garis Tangen |
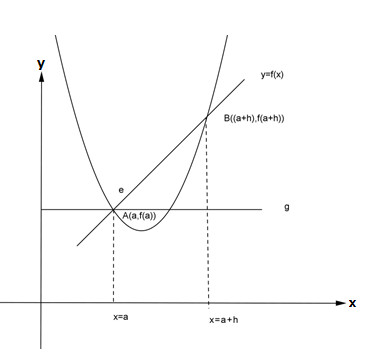
Mari kita ingat sejenak materi tentang gradien garis singgung melalui gambar di bawah ini.

Pada gambar di atas, gradien garis AB adalah
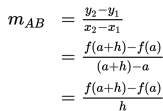
Apabila garis AB diputar pada titik A, maka titik B akan bergerak mendekati titik A yang mengakibatkan nilai h mendekati nol (h → 0) dan tali busur AB menjadi garis singgung g pada kurva y = f(x) di titik A(a, f(a)) dengan gradien sebagai berikut :
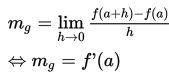
Dengan demikian, dapat kita simpulkan bahwa persamaan garis singgung pada kurva y = f(x) di titik A(x1 , y1) adalah
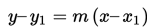
Agar kalian lebih mudah dalam memahami tafsiran geometris suatu turunan garis tangen, mari kita cermati beberapa contoh berikut ini.
Contoh 1 :
Diketahui kurva y = x2 – 3x + 4 dan titik A (3,4).
a. Tentukan gradient garis singgung di titik A.
b. Tentukan persamaan garis singgung di titik A.
b. Tentukan persamaan garis singgung di titik A.
Penyelesaian :
Oleh karena persamaan kurva adalah y = x2 – 3x + 4, maka turunan pertamanya adalah
y' = 2x - 3.
y' = 2x - 3.
a. Gradien di titik A (3,4)
- Gradien di titik A (3,4) sama dengan nilai y' untuk x = 3
- m = y’ |x = 3 = 2(3) – 3 = 6 – 3 = 3
b. Persamaan garis singgung di titik A (3,4)
Persamaan garis singgung di titik (x1 , y1) = (3,4) adalah sebagai berikut :
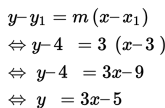
Contoh 2 :
Diketahui garis singgung pada kurva y = x2 + 2x - 10 mempunyai gradien 12. Tentukan titik singgungnya kurva tersebut!
Penyelesaian :
Turunan pertama kurva y = x2 + 2x - 10 adalah y' = 2x + 2.
Jika dimisalkan titik singgung kurva adalah (a,b), maka
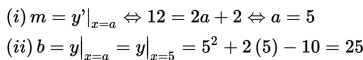
Dengan demikian, titik singgung kurva adalah (5,25).
Contoh 3 :
Diketahui garis singgung dari kurva y = ax2 + bx + 8 di titik (1,10) mempunyai gradien 3. Tentukan nilai a dan b !
Penyelesaian :
Turunan pertama kurva y = ax2 + bx + 8 adalah y' = 2ax + b.
Oleh karena gradien garis singgung kurva di titik (1,10) adalah 3, maka
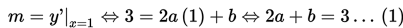
Selanjutnya, karena titik singgung kurva adalah (1,10), maka untuk x = 1 diperoleh y = 10.
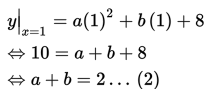
Jika persamaan (1) dan (2) kita eliminasi, maka diperoleh a = 1 dan b = 1.