Tafsiran Geometris Suatu Turunan Garis Normal
Tafsiran Geometris Suatu Turunan Garis Normal - Pada topik sebelumnya kalian sudah mengetahui cara menentukan gradien sebuah garis singgung. Selain itu kalian juga mempelajari bagaimana menyusun persamaan garis singgung sebuah kurva.
Pada topik ini kalian akan mempelajari tentang penggunaan turunan untuk menentukan persamaan garis normal. Apa itu garis normal? Apa hubungannya garis normal dengan garis tangen? Kalian akan mendapat jawabannya pada materi kali ini.
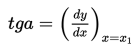
Persamaan tangen di titik P(x₁ , y₁) pada kurva y =f(x ) adalah:
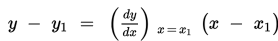
Persamaan normal di titik P(x₁ , y₁) pada kurva y =f(x ) adalah:
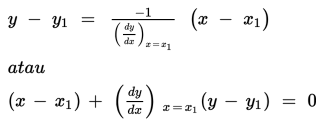
Contoh 1:
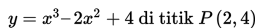

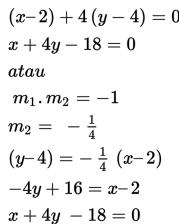
Contoh 2:
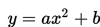
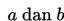

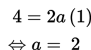
Contoh 3:

 |
| Tafsiran Geometris Suatu Turunan Garis Normal |
Pada topik ini kalian akan mempelajari tentang penggunaan turunan untuk menentukan persamaan garis normal. Apa itu garis normal? Apa hubungannya garis normal dengan garis tangen? Kalian akan mendapat jawabannya pada materi kali ini.
Persamaan Garis Normal
Garis normal adalah garis yang tegak lurus dengan garis singgung (tangen) kurva
pada P(x₁ , y₁)
pada P(x₁ , y₁)
Jika P(x₁ , y₁) terletak pada kurva y = f(x ) maka
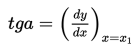
Persamaan tangen di titik P(x₁ , y₁) pada kurva y =f(x ) adalah:
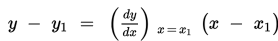
Persamaan normal di titik P(x₁ , y₁) pada kurva y =f(x ) adalah:
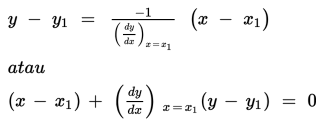
Nah, supaya lebih jelas penjelasannya silakan kalian cermati contoh berikut:
Contoh 1:
Tentukan persamaan tangen dan normal pada kurva:
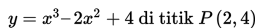
Penyelesaian:

Persamaan garis normal
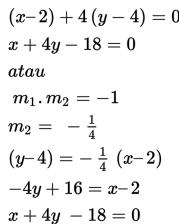
Contoh 2:
Jika garis singgung pada kurva
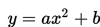
di titik (1,0) mempunyai gradien 4 maka nilai
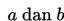
masing-masing ….
Penyelesaian:

gradien garis sunggung di titik (1, 0) adalah 4.
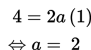
Persamaan kurva menjadi y = 10 x2 + b
Kurva melalui titik (1, 0) maka
0 = 10. 12 + b
b = −10
Kurva melalui titik (1, 0) maka
0 = 10. 12 + b
b = −10
Contoh 3:
Diketahui sebuah garis menyinggung kurva y = −x2 dan sejajar dengan garis g: 4x + y + 3 = 0. Tentukan persamaan garis normalnya.
Penyelesaian:
garis g: 4x + y + 3 = 0 mempunyai gradien m₁ = −4
Kurva y = −x2 mempunyai gradien garis singgung m₂ = y' = −2x
Kurva y = −x2 mempunyai gradien garis singgung m₂ = y' = −2x
Garis sejajar garis singgung kurva maka m₁ = m₂
−2x = 2
x = −1
−2x = 2
x = −1
untuk x = −1 maka y = −(−1)2 = −1
Persamaan garis singgung yang melalui (−1, −1) dan bergradien 2:
y+1 = 2(x +1)
y = 2x + 2 −1
y = 2x + 1
y = 2x + 2 −1
y = 2x + 1
