Aturan Sinus dan Cosinus Untuk Mencari Sudut
Aturan Sinus dan Cosinus Untuk Mencari Sudut - Seperti yang sudah diketahui pada pelajaran 205 dan 206, dasar dari aturan sinus dan cosinus adalah sama. Kamu hanya perlu menyesuaikan dengan keadaa yang diberikan soal dan merubah bentuk rumusnya untuk menentukan sudut dan panjang sisi dari segitiga apapun.
Menggunakan aturan sinus untuk menentukan sudut
Pada pelajaran kali ini kamu akan mempelejari cara menentukan sudut dengan menggunakan aturan sinus, jika dua panjang sisi dan satu sudut diberikan, maka gunakan perbandingan sinus dengan sudut berada di atas.
sinA/a = sinB/b = sinC/c
Dengan cara yang sama dengan pelajaran sebelumnya kamu TIDAK perlu menyebutkan semua perbandingan rumus sinus karena kamu hanya akan membutuhkan dua sudut dan dua sisi dalam satu hal.
sinA/a = sinB/b
Menggunakan aturan cosinus untuk menentukan sudut
Demikian yang telah kamu pelajari di atas tentang aturan sinus, menggunakan aturan cosinus dalam menentukan sudut kamu perlu untuk merubah bentuk rumusnya sehingga cos dari sudut adalah subjek dari rumus.
sinA= (b2 + c2 - a2) / 2bc
sinB= (a2 + c2 - b2) / 2ac
sinC= (a2 + b2 - c2) / 2ab
Contoh 1
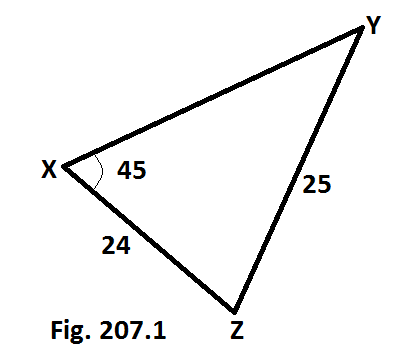
Tentukan besar sudut Y dari segitiga berikut. [Fig. 207.1]
 |
| Aturan Sinus dan Cosinus Untuk Mencari Sudut |
Menggunakan aturan sinus untuk menentukan sudut
Pada pelajaran kali ini kamu akan mempelejari cara menentukan sudut dengan menggunakan aturan sinus, jika dua panjang sisi dan satu sudut diberikan, maka gunakan perbandingan sinus dengan sudut berada di atas.
sinA/a = sinB/b = sinC/c
Dengan cara yang sama dengan pelajaran sebelumnya kamu TIDAK perlu menyebutkan semua perbandingan rumus sinus karena kamu hanya akan membutuhkan dua sudut dan dua sisi dalam satu hal.
sinA/a = sinB/b
Menggunakan aturan cosinus untuk menentukan sudut
Demikian yang telah kamu pelajari di atas tentang aturan sinus, menggunakan aturan cosinus dalam menentukan sudut kamu perlu untuk merubah bentuk rumusnya sehingga cos dari sudut adalah subjek dari rumus.
sinA= (b2 + c2 - a2) / 2bc
sinB= (a2 + c2 - b2) / 2ac
sinC= (a2 + b2 - c2) / 2ab
Contoh 1
Tentukan besar sudut Y dari segitiga berikut. [Fig. 207.1]
A 48.6∘
B 49.4∘
C 40.2∘
D 46.7∘
B 49.4∘
C 40.2∘
D 46.7∘
E 42.8∘
Jawaban E

Penjelasan
sinA/a = sinB/b
--> sinX/x = sinY/y
--> sin45/25 = sinY/24
--> ∡ Y = 42.75 ≃ 42.8∘
Contoh 2
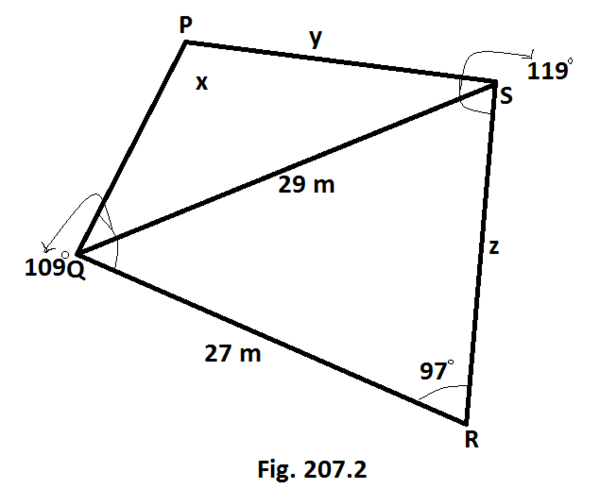
Tentukan nilai x, y dan z trapesium pada [Gb.207.2]
sinA/a = sinB/b
--> sinX/x = sinY/y
--> sin45/25 = sinY/24
--> ∡ Y = 42.75 ≃ 42.8∘
Contoh 2
Tentukan nilai x, y dan z trapesium pada [Gb.207.2]

A ∡ x = 35∘ , y = 50.5 m ,z = 7.8 m
B ∡ x = 35∘ , y = 50.2 m ,z = 7.8 m
C ∡ x = 93.5∘ ,y = 40.7 m ,z = 7.6 m
D ∡ x = 34∘ ,y = 50.3 m ,z = 7.4 m
E ∡ x = 34∘ , y = 50.5 m ,z = 7.6 m
Jawaban A
Penjelasan
Perhatikan △
B ∡ x = 35∘ , y = 50.2 m ,z = 7.8 m
C ∡ x = 93.5∘ ,y = 40.7 m ,z = 7.6 m
D ∡ x = 34∘ ,y = 50.3 m ,z = 7.4 m
E ∡ x = 34∘ , y = 50.5 m ,z = 7.6 m
Jawaban A
Penjelasan
Perhatikan △
QRS,
kita mempunyai
--> sinS/27 = sin97/29
--> ∡S = 67.53 ≃ 67.5∘
Sehingga, ∡Q = 180∘ - 97∘ - 67.5∘ = 15.46∘ ≃ 15.5∘
Sekarang, kita dapat menentukan z menggunakan aturan sinus:
sinQ/q = sinR/r
--> sin 15.5/z = sin97/29
--> z = 7.808 ≃ 7.8 m
Untuk menentukan nilai-nilai lainnya yang belum diketahui, perhatikan △PQS sebagai berikut:
--> ∡Q in △PQS = 109∘ - 15.5∘ = 93.5∘,
--> ∡S in △PQS = 119∘ - 67.5∘ = 51.5∘, dan
--> ∡X in △PQS = 180∘ - 51.5∘ = 35∘
Terakhir, gunakan aturan sinus untu menentukan panjang Y:
x/sinX = y/sinY
--> 29/sin35 = y/sin93.5
--> y = 50.46 ≃ 50.5 m
Contoh 3
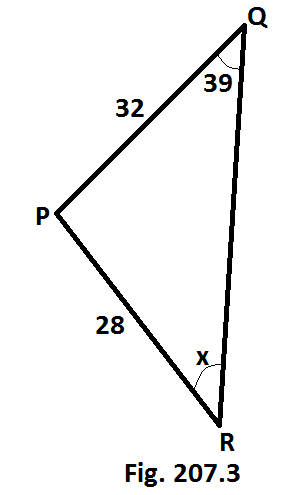
Tentukan besar sudut R dari segitiga berikut. [Gb. 207.3]
--> ∡S = 67.53 ≃ 67.5∘
Sehingga, ∡Q = 180∘ - 97∘ - 67.5∘ = 15.46∘ ≃ 15.5∘
Sekarang, kita dapat menentukan z menggunakan aturan sinus:
sinQ/q = sinR/r
--> sin 15.5/z = sin97/29
--> z = 7.808 ≃ 7.8 m
Untuk menentukan nilai-nilai lainnya yang belum diketahui, perhatikan △PQS sebagai berikut:
--> ∡Q in △PQS = 109∘ - 15.5∘ = 93.5∘,
--> ∡S in △PQS = 119∘ - 67.5∘ = 51.5∘, dan
--> ∡X in △PQS = 180∘ - 51.5∘ = 35∘
Terakhir, gunakan aturan sinus untu menentukan panjang Y:
x/sinX = y/sinY
--> 29/sin35 = y/sin93.5
--> y = 50.46 ≃ 50.5 m
Contoh 3
Tentukan besar sudut R dari segitiga berikut. [Gb. 207.3]

A 41∘
B 39∘
C 45∘
D 46∘
E 50∘
Jawaban D
Penjelasan
Dimulai dengan aturan sinus, kita dapatkan
sinQ/q = sinR/r
--> sin39/28 = sinR/32
--> sinR = 0.719
--> ∡ R = 45.99∘ ≃ 46∘
tapi, ada kemungkinan satu sudut memiliki sinus sama dengan 0.7192.
Kamu dapat menentukannya dengan mengurangkan sudut lancip dari180∘, sebagai berikut:
--> 180∘ - 46∘ = 134∘
Kamu juga bisa memeriksanya dengan menghitung nilai sin 134 menggunakan alat bantu kalkulator.
--> sin134 = 0.719
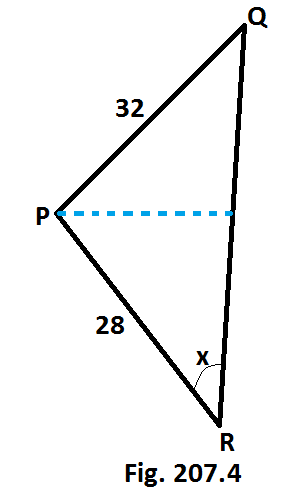
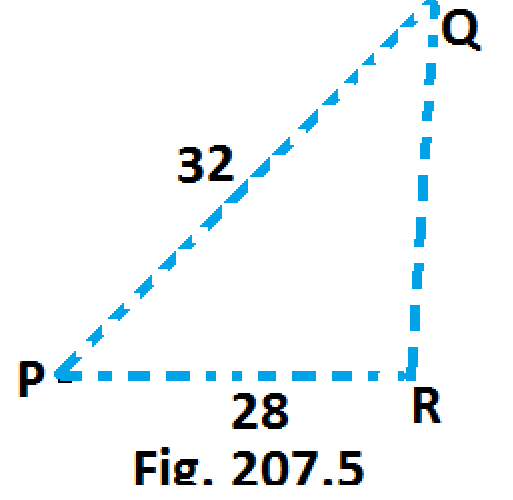
Jadi, ada dua kemungkinan nilai untuk ∡ R. [Lihat Gb. 207.4 & Fig. 207.5]
B 39∘
C 45∘
D 46∘
E 50∘
Jawaban D
Penjelasan
Dimulai dengan aturan sinus, kita dapatkan
sinQ/q = sinR/r
--> sin39/28 = sinR/32
--> sinR = 0.719
--> ∡ R = 45.99∘ ≃ 46∘
tapi, ada kemungkinan satu sudut memiliki sinus sama dengan 0.7192.
Kamu dapat menentukannya dengan mengurangkan sudut lancip dari180∘, sebagai berikut:
--> 180∘ - 46∘ = 134∘
Kamu juga bisa memeriksanya dengan menghitung nilai sin 134 menggunakan alat bantu kalkulator.
--> sin134 = 0.719
Jadi, ada dua kemungkinan nilai untuk ∡ R. [Lihat Gb. 207.4 & Fig. 207.5]


Oleh karena itu, kamu perlu berhati-hati untuk melihat ada tidaknya kemungkinan jawaban untuk dipertimbangkan!