Mengenal Deret Persegi dan Deret Kubik

Mengenal Deret Persegi dan Deret Kubik - Masih ingatkah kalian dengan barisan bilangan kuadrat dan barisan bilangan pangkat tiga?

Mengenal Deret Persegi dan Deret Kubik

Ya, barisan bilangan kuadrat adalah 12,22,32,42,...=1,4,9,16,...$1^2,2^2,3^2,4^2,...=1,4,9,16,...$ dan barisan bilangan pangkat tiga adalah 13,23,33,43,...=1,8,27,64,...$1^3,2^3,3^3,4^3,...=1,8,27,64,...$.

Nah, untuk selanjutnya, barisan bilangan kuadrat disebut dengan barisan persegi dan barisan bilangan pangkat tiga disebut barisan kubik.

Deret Persegi

Apakah kalian masih ingat dengan bentuk noktah dari bilangan persegi?

Yuk kita cermati noktah berikut.

Secara umum, deret persegi sampai dengan suku ke-n$n$ dapat ditulis dalam bentuk berikut: 1+4+9+16+...+n2$1+4+9+16+...+n^2$

Adapun jumlah n$n$ suku pertama dari deret persegi adalah Sn=∑k=1nk2=16n(n+1)(2n+1)$S_n=\sum _{k=1}^n{k}^2=\frac{1}{6}n\left(n+1\right)\left(2n+1\right)$.

Ingat, n=1,2,...$n=1,2,...$.

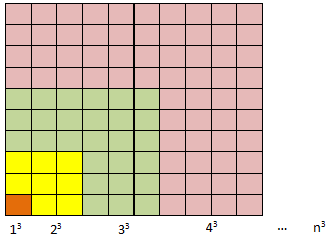
Deret Kubik

Pola bilangan kubik ditunjukkan oleh ilustrasi berikut:

Nah, deret kubik sampai dengan suku ke-n$n$ adalah 1+8+27+64+...+n3$1+8+27+64+...+n^3$

Adapun jumlah n$n$ suku pertama dari deret kubik adalah Sn=∑k=1nk3=14n2(n+1)2$S_n=\sum _{k=1}^n{k}^3=\frac{1}{4}{n}^2{\left(n+1\right)}^2$.

Ingat, n=1,2,...$n=1,2,...$.

Agar kalian lebih paham dengan materi di atas, yuk kita cermati beberapa contoh soal berikut ini.

Contoh 1

Diketahui deret bilangan: 0 + 1 + 4 + 9 + ….
Tentukan suku ke-10 dan jumlah sepuluh suku pertama dari deret tersebut.

Penyelesaian:

Jika kita jabarkan deret bilangan pada soal, maka kita peroleh pola sebagai berikut:

• suku ke-1 = 02=(1–1)2$0^2=(1–1{)}^2$
• suku ke-2 = 12=(2–1)2$1^2=(2–1{)}^2$
• suku ke-3 = 22=(3–1)2$2^2=(3–1{)}^2$
• suku ke-4 = 32=(4–1)2$3^2=(4–1{)}^2$

Berdasarkan pola di atas, dapat kita simpulkan bahwa suku ke-10 dari deret bilangan: 0+1+4+9+…$0+1+4+9+\dots$ adalah (10–1)2=92=81$(10–1{)}^2=9^2=81$.

Adapun jumlah sepuluh suku pertama dari deret bilangan: 0+1+4+9+…$0+1+4+9+\dots$ adalah

0+1+4+9+16+25+36+49+64+81=285$0+1+4+9+16+25+36+49+64+81=$

$285$

Pelu kalian ketahui, kalian juga dapat menggunakan rumus Un$U_n$ dan Sn$S_n$ untuk menyelesaikan soal di atas.

Bagaimanakah caranya?
Yuk kita cermati penyelesaian berikut.

Oleh karena suku ke-n$n$ dari deret persegi 1+4+9+16+...$1+4+9+16+...$ adalah Un=n2$U_n=n^2$, maka suku ke-n$n$ dari deret persegi 0+1+4+9+...=(1−1)2+(2−1)2+(3−1)2+(4−1)2+...$0+1+4+9+...$

$=(1-1{)}^2+(2-1{)}^2+(3-1{)}^2+(4-1{)}^2+...$ adalah Un=(n−1)2$U_n=(n-1{)}^2$, dengan n=1,2,...$n=1,2,...$.

Dengan demikian, suku ke-10 dari deret persegi: 0+1+4+9+...$0+1+4+9+...$ adalah U10=(10−1)2=92=81${U_1}_0=(10-1{)}^2=9^2=81$.

Selanjutnya, karena jumlah n$n$ suku pertama dari deret persegi: 1+4+9+16+...$1+4+9+16+...$adalah Sn=16n(n+1)(2n+1)$S_n=\frac{1}{6}n\left(n+1\right)\left(2n+1\right)$, maka jumlah n$n$ suku pertama dari deret persegi: 0+1+4+9+...=(1−1)2+(2−1)2+(3−1)2+(4−1)2+...$0+1+4+9+...$

$=(1-1{)}^2+(2-1{)}^2+(3-1{)}^2+(4-1{)}^2+...$ adalah Sn=16(n−1)((n−1)+1)(2(n−1)+1)=16(n−1)(n)(2n−1)$S_n$

$=\frac{1}{6}(n-1)\left((n-1)+1\right)\left(2(n-1)+1\right)=\frac{1}{6}(n-1)\left(n\right)\left(2n-1\right)$, dengan n=1,2,...$n=1,2,...$.

Dengan demikian,

S10=16(10−1)(10)(2(10)−1)=16×9×10×19=285${S_1}_0=\frac{1}{6}(10-1)(10)(2(10)-1)$

$=\frac{1}{6}\times 9\times 10\times 19=285$

Contoh 2

Diketahui deret bilangan kubik: 1 + 8 + 27 + …. Tentukan jumlah sepuluh suku pertama dari deret tersebut.

Penyelesaian:

Oleh karena rumus jumlah n$n$ suku pertama dari deret kubik: 1+8+27+...$1+8+27+...$ adalah Sn=14n2(n+1)2$S_n=\frac{1}{4}{n}^2(n+1{)}^2$, maka S10=14(10)2(10+1)2=14×100×121=3.025${S_1}_0=\frac{1}{4}(10{)}^2(10+1{)}^2$

$=\frac{1}{4}\times 100\times 121=3.025$

Yuk kerjakan sepuluh latihan soal yang ada dalam topik ini untuk menguji pemahan kalian.

Share this post