Contoh Soal Uji Hipotesis Dua Pihak
Contoh Soal Uji Hipotesis Dua Pihak - Hipotesis adalah asumsi atau dugaan mengenai sesuatu hal. Hipotesis bisa benar ataupun tidak benar. Untuk menentukan apakah hipotesis itu benar atau tidak benar, dapat ditempuh dengan melakukan pengujian hipotesis.
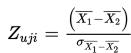

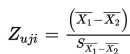


Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
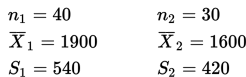
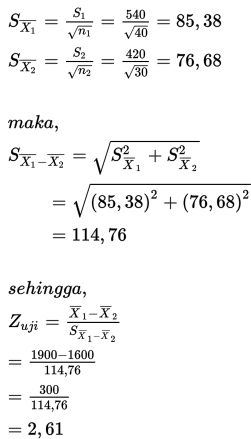
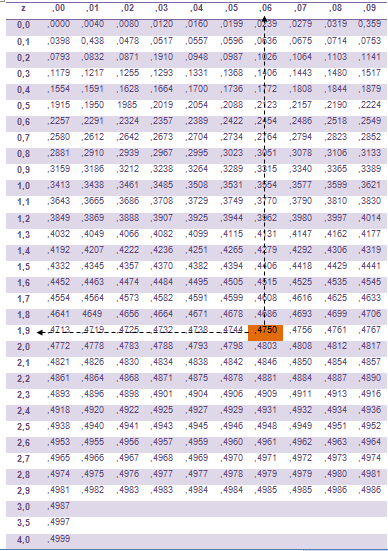
Tabel Distribusi Normal Standar (Tabel Z)
Contoh 2 :

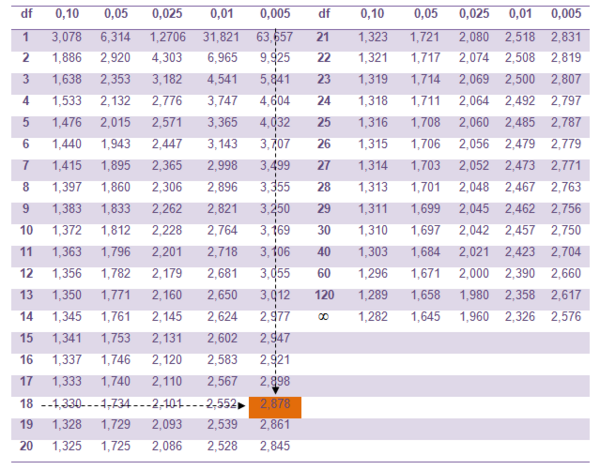
Tabel Distribusi t-student
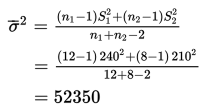
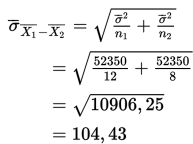
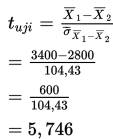
Contoh 3 :
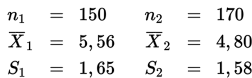
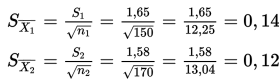
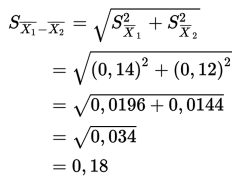
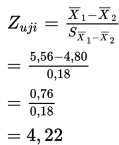
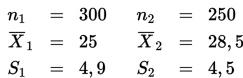
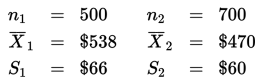
Uji hipotesis beda dua mean populasi dengan distribusi normal
Langkah-langkah pengujian hipotesis adalah sebagai berikut :
1. Penentuan H0 dan H1
- H0 : μ1 - μ2 = 0 atau μ1 = μ2
- H1 : μ1 - μ2 ≠ 0 atau μ1 ≠ μ2
2. Penentuan Zkritis
3. Penentuan Zuji
3. Penentuan Zuji
- Kemungkinan pertama (yang diketahui adalah σ1 dan σ2)
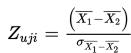
dengan

- Kemungkinan kedua (yang diketahui adalah S1 dan S2)
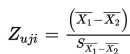
dengan

4. Pengambilan keputusan
Terima H0 jika
- Zkritis bawah ≤ Zuji ≤ Zkritis atas
Tolak H0 jika :
- Zuji < Zkritis bawah
- Zuji > Zkritis atas
Uji hipotesis beda dua mean populasi dengan distribusi t-student
Distribusi t untuk uji hipotesis beda dua mean digunakan jika kondisi yang dihadapi adalah sebagai berikut:
- Standar deviasi populasi σ tidak diketahui (yang diketahui adalah s)
- Sampelnya kecil (n < 30)
- Populasinya dianggap berdistribusi normal
- Standar deviasi dari dua populasi yang tidak diketahui besarnya tersebut adalah sama besarnya (σ1 = σ2)
Hal-hal penting dalam pengujian beda dua mean dengan distribusi t:
- Penentuan nilai tkritis tergantung dari derajat keyakinan dan derajat bebas. Dalam hal ini derajat bebasnya adalah n1 + n2 – 2
- Penentuan tuji diperoleh dari rumus :

Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Terdapat dugaan bahwa mean pendapatan rumah-tangga bulanan dari kota A dan kota B adalah sama. Seseorang ingin menguji hipotesis tersebut dengan mengumpulkan data sebagai berikut. Dari kota A diambil 40 anggota keluargasebagai sampel, dan didapat mean pendapatan bulanannya $1,900 dengan standar deviasi $540. Dari kota B diambil 30 anggota keluarga sebagai sampel, dan didapat mean pendapatan bulanannya $1.600 dengan standar deviasi $420.
Bantulah orang tersebut dalam melakukan uji hipotesisnya dengan menggunakan derajat keyakinan 95% !
Penyelesaian :
Diketahui :
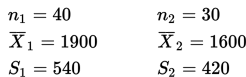
1. Penentuan H0 dan H1
H0 : μ1 = μ2 (mean pendapatan rumah tangga bulanan dari kota A dan kota B
adalah sama)
H1 : μ1 ≠ μ2
adalah sama)
H1 : μ1 ≠ μ2
2. Penentuan nilai kritis
dk = 95% = 0,95
Karena uji 2 pihak maka yang kita gunakan hanyalah ½ dk = ½ (0,95) = 0,475 , sehingga Zkritis = ±1,96 (lihat tabel Z)
3. Penentuan nilai uji
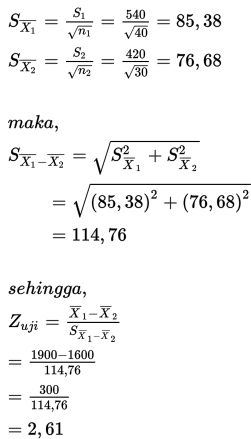
4. Karena 2,61 > + 1,96 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa mean pendapatan dua kota tersebut sama adalah tidak benar.
Kesimpulannya, pernyataan bahwa mean pendapatan dua kota tersebut sama adalah tidak benar.
Tabel Distribusi Normal Standar (Tabel Z)

Contoh 2 :
Diduga bahwa tidak ada beda antara mean daya tahan hidup dua merk batu baterai, yaitu merk A dan B. Untuk menguji hipotesis tersebut telah dikumpulkan data sebagai berikut: n1 = 12, X1= 3.400 jam, S1 = 240 jam, n2 = 8, X2= 2.800 jam, S2 = 210 jam. Bagaimana hasil ujinya? Gunakan derajat keyakinan 99%.
Penyelesaian :
1. Penentuan H0 dan H1
- H0 : μ1 = μ2 (tidak ada beda antara mean daya tahan hidup dua merk batu baterai)
- H1 : μ1 ≠ μ2
2. Penentuan nilai kritis

Tabel Distribusi t-student

3. Penentuan nilai uji
Dugaan atas variansi populasi gabungan 2 populasi :
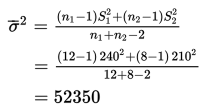
Standar deviasi sampling :
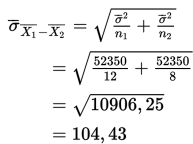
sehingga
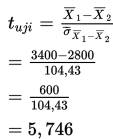
4. Karena 5,746> + 2,878 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa tidak ada beda antara mean daya tahan hidup dua merk baterai adalah tidak benar.
Contoh 3 :
Informasi-informasi berikut ini diperoleh dari dua sampel independen dari dua buah populasi.
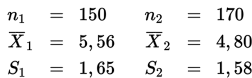
Dengan informasi tersebut, ujilah hipotesis bahwa dua mean populasi adalah berbeda. Gunakan tingkat signifikansi 5%.
Penyelesaian :
1. Penentuan H0 dan H1
- H0 : μ1 = μ2 (dua mean populasi adalah berbeda)
- H1 : μ1 ≠ μ2
2. Penentuan nilai kritis
- α = 0,05 maka Zkritis = ± 1,96
3. Penentuan nilai uji
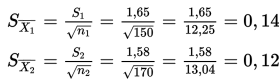
maka
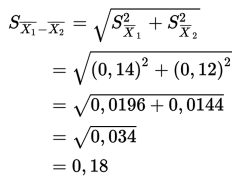
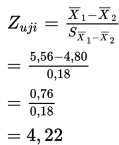
4. Karena 4,22 > + 1,96 maka kita menolak H0.
Kesimpulannya, pernyataan bahwa mean dua populasi berbeda adalah tidak benar.
S1
Sebuah perusahaan baru saja membuka dua buah supermarket di dua tempat yang berbeda. Pihak manajemen perusahaan tersebut ingin mengetahui apakah mean penjualan per hari dari dua supermarket tersebut berbeda. Sebuah sampel diambil dari supermarket pertama berupa 35 hari kerja menghasilkan mean penjualan perhari sebesar $53,70 dengan standar deviasi $2,90. Sebuah sampel diambil dari supermarket kedua berupa 30 hari kerja menghasilkan mean penjualan per hari sebesar $58,45 dengan standar deviasi $3,10. Dengan tingkat signifikansi 1%, kesimpulan berikut yang benar adalah ....
S2
Menurut biro Pusat Statistik suatu negara, mean pendapatan penduduk negara itu pada tahun 1988 adalah $38.608 dan pada tahun 1991 adalah $43.704. Asumsikan kedua mean pada dua tahun tersebut didasarkan pada sampel random dengan ukuran 1.800 pada tahun 1988 dan 2.200 pada tahun 1991. Asumsikan pula bahwa standar deviasi pada dua tahun tersebut berturut-turut adalah $9.569 dan $9.885. Dengan tingkat signifikansi 5% akan diuji hipotesis bahwa mean tingkat pendapatan penduduk pada tahun 1988 adalah berbeda dengan mean tingkat pendapatan penduduk pada tahun 1991. Pernyataan yang benar adalah ...
S3
Pihak Manajemen Bank A menyatakan bahwa mean waktu tunggu pelayanan nasabah dibank tersebut adalah lebih kecil dari pada meanwaktu tunggu pelayanan nasabah di bank B (catatan, bank B adalah pesaing dari bank A). Sebuah lembaga independen bermaksud menguji pernyataan tersebut. Dari bank A diambil sampel random sejumlah 200 nasabah dan didapatkan mean waktu tunggunya adalah 4,85 menit dengan standar deviasi 6,3 menit. Dengan tingkat signifikansi 1%, pernyataan yang benar adalah ...
S4
Informasi-informasi berikut ini diperoleh dari dua sampel independen dari dua buah populasi.
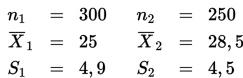
Akan diuji hipotesis bahwa dua mean populasi adalah berbeda dengan tingkat signifikansi 5%. Pernyataan yang benar adalah ...
S5
Biro Pusat Statistik suatu negara ingin mengetahui upah per jam dari pekerja tambang dan pekerja transportasi. Untuk itu dikumpulkan sampel 1.100 pekerja tambang dan didapatkan mean pendapatannya adalah $14,51 dengan standar deviasi $1,55. Dari pekerja transportasi dikumpulkan sampel 1.400 buruh tambang dan didapatkan mean pendapatannya adalah $13,49 dengan standar deviasi $1,78. Jika diasumsikan upah buruh per jam dari dua populasi tersebut berdistribusi normal, akan diuji dengan tingkat signifikansi 1% bahwa mean upah per jam di sektor pertambangan adalah lebih tinggi dari pada mean upah per jam di sektor transportasi. Pernyataan yang benar adalah ...
S6
Berikut ini data sampel tentang pendapatan per minggu yang diambil dari dua populasi kelompok pegawai, yaitu pegawai bangunan (I) dan pegawai pabrik (II):
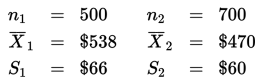
Akan diuji pernyataan bahwa mean pendapatan per minggu kelompok pegawai bangunan adalah sama dengan mean pendapatan per minggu kelompokpegawai pabrik. Dengan derajat keyakinan 95%, pernyataan yang benar adalah ...
S7
Untuk sampel random berjumlah 10 buah lampu dari sebuah merk, mean umur bola lampu adalah4.600 jam dengan standar deviasi 250 jam. Untuk bola lampu merk yang lain, mean umur bola lampu dari sampel sejumlah 8 adalah 4.000 jam dan standar deviasi 200 jam. Dengan tingkat signifikansi 5% akan diuji hipotesis bahwa mean umur bola lampu merk pertama adalah tidak berbeda dengan mean umur bola lampu merk kedua. Pernyataan yang benar adalah ...
S8
Seorang peneliti ingin mengetahui perbedaan IPK (Indeks Prestasi Kumulatif) dari mahasiswa yang bekerja sambil kuliah dan mahasiswa yang tidak bekerja. Untuk itu dikumpulkan sampel berupa 28 mahasiswa yang bekerja sambil kuliah dan didapatkan mean IPK 2,62 dengan standar deviasi 0,43. Dari siswa yang tidak bekerja dikumpulkan sampel sejumlah 24 siswa dan didapatkan mean IPK 2,74 dengan standar deviasi 0,38. Misalnya diasumsikan bahwa IPK dari dua kelompok siswa tersebut berdistribusi normal. Dengan tingkat signifikansi 5% akan diuji hipotesis bahwa mean IPK siswa yang bekerja sambil kuliah adalah kurang dari mean IPK siswa yang tidak bekerja ketika kuliah. Pernyataan yang benar adalah ...
S9
Informasi-informasi berikut ini diperoleh dari dua sampel independen dari dua buah populasi yang berdistribusi normal dengan standar deviasi yang tidak diketahui besarnya, tetapi diasumsikan sama besarnya.
Sampel 1: 13 ; 11 ; 9 ; 12 ; 8 ; 10 ; 5 ; 10 ; 9 ; 12 ; 13
Sampel 2: 16 ; 14 ; 11 ; 19 ; 14 ; 17 ; 13 ; 16 ; 17 ; 18 ; 19 ; 12
Sampel 2: 16 ; 14 ; 11 ; 19 ; 14 ; 17 ; 13 ; 16 ; 17 ; 18 ; 19 ; 12
Akan diuji hipotesis bahwa η1 adalah lebih dari η2. Dengan menggunakan α = 1%, pernyataan yang benar adalah ....
S10
Sebuah perusahaan asuransiingin mengetahui apakah mean kecepatan pria dalam mengemudi mobil lebih dari mean kecepatan wanita. Perusahaan tersebut mengambil 27 mobil yang dikendarai pribadi sebuah jalanbesar secara random dan mendapatkan mean kecepatannya adalah 68 mil per jam denganstandar deviasi 2,2 mil per jam. Perusahaan tersebut juga mengambil 18 mobil yang dikendarai wanita di jalan besar yang samadan mendapatkan mean kecepatannya adalah 65 mil per jam dengan standar deviasi 2,5 mil per jam. Jika diasumsikan bahwakecepatan mengendara mobil pria dan wanita berdistribusi normal, akan diuji hipotesis bahwa mean kecepatan pria dalam mengendarai mobil adalah lebih tinggi daripada mean kecepatan wanita dalam mengendarai mobil. Dengan tingkat signifikansi 1%, pernyataan yang benar adalah ....
