Contoh Soal Masalah nyata yang berkaitan dengan turunan fungsi trigonometri
Contoh Soal Masalah nyata yang berkaitan dengan turunan fungsi trigonometri - Pada topik sebelumnya kalian telah belajar tentang konsep turunan fungsi aljabar dan fungsi trigonometri. Kalian juga telah belajar menerapkan konsep turunan fungsi aljabar untuk masalah nyata maupun masalah matematika.
Apakah kalian masih ingat terapan konsep turunan digunakan untuk apa?
Agar lebih jelas mari kita perhatikan contoh berikut ini.
Contoh :
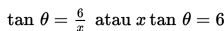
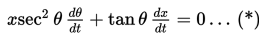
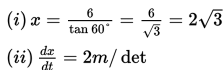
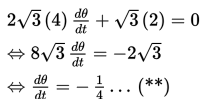
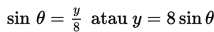
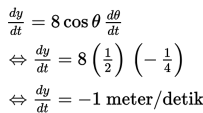
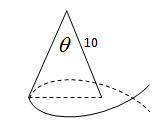
Apakah kalian masih ingat terapan konsep turunan digunakan untuk apa?
Penerapan konsep turunan antara lain dipakai untuk :
1) menentukan persamaan garis singgung kurva
2) menentukan interval dimana fungsi naik dan interval dimana fungsi turun
3) menentukan menyelesaikan masalah-masalah ekstrim
4) menentukan gerak rektilinear (kecepatan dan percepatan pada gerak lurus)
5) perhitungan pada limit fungsi
1) menentukan persamaan garis singgung kurva
2) menentukan interval dimana fungsi naik dan interval dimana fungsi turun
3) menentukan menyelesaikan masalah-masalah ekstrim
4) menentukan gerak rektilinear (kecepatan dan percepatan pada gerak lurus)
5) perhitungan pada limit fungsi
Nah, pada topik kali ini, kalian akan belajar menyelesaikan masalah-masalah nyata yang berkaitan dengan turunan fungsi trigonometri.
Dalam hal ini, tentu kalian harus ingat turunan fungsi trigonometri, antara lain :
- turunan fungsi y = sin x adalah y’ = cos x
- turunan fungsi y = cos x adalah y’ = - sin x
- turunan fungsi y = tan x adalah y’ = sec2 x, dan seterusnya.
Agar lebih jelas mari kita perhatikan contoh berikut ini.
Contoh :
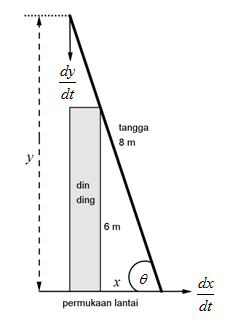
Sebuah tangga panjangnya 8 meter bersandar pada dinding tegak yang tingginya 6 meter dengan bagian atas tangga melewati dinding. Jika ujung bawahnya ditarik horizontal dengan kecepatan 2 meter/detik menjauhi dinding, tentukan kecepatan vertikal ujung atas tangga pada saat tangga membentuk sudut 60o dengan permukaan lantai.
Penyelesaian :
Perhatikan gambar berikut :

Misalkan pada saat t, sudut antara tangga dengan permukaan lantai adalah ϴ, jarak ujung bawah tangga ke dinding adalah x meter, dan jarak ujung atas tangga ke permukaan lantai adalah y meter.
Oleh karena kecepatan vertikal ujung atas tangga ditanyakan, maka kita perlu menentukan dy/dt pada saat tangga membentuk sudut 60o dengan permukaan lantai dan dx/dt = 2 m/det.
Berdasarkan gambar di atas,
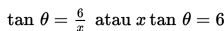
Turunan implisit terhadap t dari kedua ruas menghasilkan
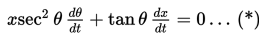
Untuk ϴ = 60o berlaku :
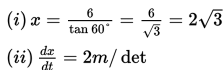
Jika hasil di atas disubtitusikan ke persamaan (*), maka diperoleh hasil sebagai berikut :
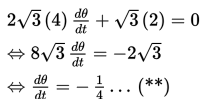
Jika kita melihat gambar di atas lagi, maka diperoleh
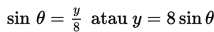
Turunan implisit terhadap t dari kedua ruas menghasilkan
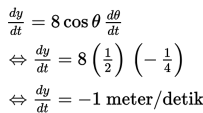
(tanda negatif menunjukkan arah ke bawah)
Dengan demikian, kecepatan vertikal ujung atas tangga adalah -1 m/det .
S1
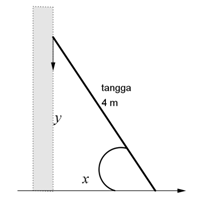
Sebuah tangga panjangnya 4 meter bersandar pada dinding tegak, ujung atasnya bersandar pada dinding dan ujung bawah terletak pada lantai mendatar. Perhatikan ilustrasi berikut:

Jika pada saat sudut antara ujung bawah tangga dengan lantai adalah 45o dan kecepatan meluncur ujung atas tangga adalah 1 meter/detik, maka kecepatan meluncur tangga di lantai adalah ….
S2
Seekor ular bergerak dipasir dan lintasannya memenuhi persamaan s = f(t) = sin 2t, t ≥ 0, dengan s dalam meter dan t dalam detik. Kecepatan gerak ular pada saat t = 1/8 πadalah …m/det.
S3
Seekor ular bergerak dipasir dan lintasannya memenuhi persamaan s = f(t) = sin 2t, t ≥ 0, dengan s dalam meter dan t dalam detik. Percepatan pada saat t = 2/3 π adalah …m/det2
S4
Dua buah kapal bergerak bersama-sama dengan arah yang berlainan. Pada waktu t detik keduanya memenuhi persamaan berikut
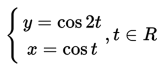
Jika kapal tersebut dihubungkan dengan sebuah garis, maka persamaan garis pada saat t = π/3 adalah ….
S5
Pada suatu pameran kedirgantaraan, dua pesawat tempur sedang melakukan gerakkan manufer di udara. Pada posisi titik tertentu dua pesawat tersebut melakukan manufer berbeda dengan arah rambatan berlawanan, dan jarak yang ditempuh mengikuti persamaan s1 = f1(t) = sin 2t dan s2 = f2(t) = -2 sin t (tanda negatif menyatakan arahnya berlawanan dengan pesawat 1). Kecepatan pesawat tersebut akan sama pada saat t = ….
S6
Sebuah mobil balap melaju pada sirkuit balap yang meliuk-liuk dengan posisinya dari titik awal ditentukan dengan persamaan s = f(t) = 20t + 20√3 sin t, t ≥ 0, dengan s dalam meter dan t dalam detik. Jarak yang ditempuh mobil balap pada kecepatan 50 m/det adalah …m.
S7
Sebuah pensil ujungnya lancip dan membentuk sudut ϴ. Perhatikan gambar berikut
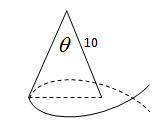
Panjang sisi miring ujung pensil adalah 10 mm. Volume maksimum ujung pensil adalah ….
S8
Sebuah pilar gedung diketahui tingginya 5 meter dan dua sisi alasnya 8 cm dan 6cm, sudut yang diapit oleh kedua sisi alas tersebut adalah ϴ. Volume pilar tersebut akan maksimum jika sudut ϴ = ….
S9
Seorang penerjun payung meluncur vertikal kebawah, pada ketinggian 200 m dia melihat perahu di sebuah danau meluncur menjauhi titik vertikal penerjun. Jarak titik dia melihat penerjun ke perahu 250 m. Jika kecepatan meluncur vertikal kebawah penerjun adalah 5 m/det, kecepatan meluncur perahu meninggalkan titik vertikal penerjun adalah ….
S10
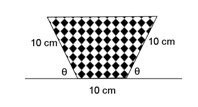
Sebuah talang air akan dibuat dari lembaran seng yang lebarnya 30 cm dengan melipat lebarnya atas menjadi 3 bagian yang sama, seperti terlihat pada gambar.

Jika ϴ menyatakan besar sudut dinding talang dengan bidang alasnya, maka volume air yang tertampung paling banyak bila ϴ = ….
