Perbandingan Ruas Garis pada Segitiga yang Sebangun

Perbandingan Ruas Garis pada Segitiga yang Sebangun - Ada beberapa macam perbandingan ruas garis pada segitiga yang sebangun yaitu perbandingan ruas garis sejajar pada segitiga, perbandingan ruas garis pada segitiga siku-siku, dan perbandingan ruas garis pada segitiga terpancung (trapesium). Agar kamu lebih paham, mari simak penjelasannya berikut ini.

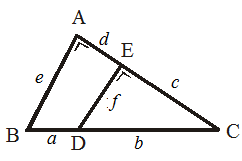
Perbandingan Ruas Garis Sejajar pada Segitiga

Perhatikan segitiga di bawah ini.

Pada segitiga tersebut, sisi f yang sejajar dengan e, sehingga diperoleh:

$\frac{c}{c+d}=\frac{a}{a+b}=\frac{e}{f}$ atau

$\frac{c}{d}=\frac{a}{b}$

Catatan: 
Kata “sejajar” juga dapat dilambangkan dengan “//”.

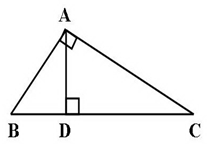
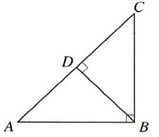
Perbandingan Ruas Garis pada Segitiga Siku-Siku

Perhatikan gambar di atas.

Pada gambar tersebut terdapat 3 pasang segitiga yang sebangun yaitu ΔBAC dengan ΔADB, ΔBAC dengan ΔADC, dan ΔADB dengan ΔADC.

• Untuk ΔBAC dan ΔADB

Perbandingan sisi–sisi yang bersesuaian adalah:

$\frac{AB}{BD}=\frac{BC}{AB}=\frac{AC}{AD}$

Dengan menggunakan $\frac{AB}{BD}=\frac{BC}{AB}$, diperoleh:

$\frac{AB}{BD}=\frac{BC}{AB}$

$\iff A{B}^2=BD\times BC$

• Untuk ΔBAC dan ΔADC

Perbandingan sisi – sisi yang bersesuaian adalah:

$\frac{AB}{AD}=\frac{CB}{AC}=\frac{AC}{CD}$

Dengan menggunakan perbandingan $\frac{CB}{AC}=\frac{AC}{CD}$, diperoleh:

$\frac{CB}{AC}=\frac{AC}{CD}$

$\iff A{C}^2=CD\times CB$

• Untuk ΔADB dan ΔADC

Perbandingan sisi–sisi yang bersesuaian adalah:

$\frac{AD}{DC}=\frac{BD}{AD}=\frac{AB}{AC}$

Dengan menggunakan perbandingan $\frac{AD}{DC}=\frac{BD}{AD}$, diperoleh:

$\frac{AD}{DC}=\frac{BD}{AD}$

$\iff A{D}^2=BD\times DC$

Berdasarkan uraian di atas, diperoleh rumus-rumus pada segitiga yang siku-siku di A sebagai berikut.

$\iff A{B}^2=BD\times BC$

$\iff A{C}^2=CD\times CB$

$\iff A{D}^2=BD\times DC$

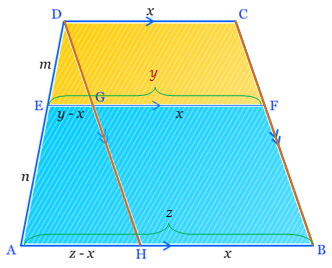
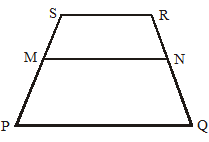
Perbandingan Ruas Garis pada Segitiga Terpancung (Trapesium)

Perhatikan gambar di bawah ini.

Oleh karena garis EG sejajar dengan garis AH, maka segitiga ΔDEG sebangun dengan segitiga ΔDAH, sehingga berlaku:

$\frac{DE}{DA}=\frac{EG}{AH}$

$\iff \frac{m}{m+n}=\frac{y-x}{z-x}$

$\iff m(z-x)=(m+n)(y-x)$

$\iff mz-mx=my-mx+ny-nx$

$\iff mz=my+ny-mx+mx-nx$

$\iff mz=(m+n)y-nx$

$\iff (m+n)y=mz+nx$

$\iff y=\frac{mz+nx}{m+n}$

Dengan demikian, pada segitiga terpancung (trapesium) ABCD berlaku:

$y=\frac{mz+nx}{m+n}$

dengan:

y = garis yang sejajar dengan dua sisi sejajar trapesium

m dan n = perbandingan ruas garis pada bukan sisi sejajar trapesium

x dan z = sisi sejajar trapesium dengan panjang x < z

◙ ◙ ◙ Contoh 1 ◙ ◙ ◙

Perhatikan gambar berikut.

Jika panjang AB = 3 cm, BC = 2 cm, dan DE = 3 cm, maka tentukan panjang BD.

Penyelesaian:

Diketahui:
panjang AB = 3 cm
panjang BC = 2 cm
panjang DE = 3 cm

Misalkan panjang BD = p.

Panjang BD dapat ditentukan dengan perbandingan ruas garis sejajar pada segitiga.

Pada segitiga tersebut, sisi DE yang sejajar dengan BC, sehingga diperoleh dua buah segitiga yang sebangun yaitu ΔADE dan ΔABC.

Ini berarti, salah satu perbandingan sisi bersesuaiannya adalah:

$\begin{array}{l}\frac{AD}{AB}=\frac{DE}{BC}\\ \iff \frac{(3+p)}{3}=\frac{3}{2}\\ \iff 2(3+p)=3(3)\\ \iff 6+2p=9\\ \iff 2p=9–6\\ \iff 2p=3\\ \iff p=1,5\end{array}$

Jadi, panjang BD = p = 1,5 cm.

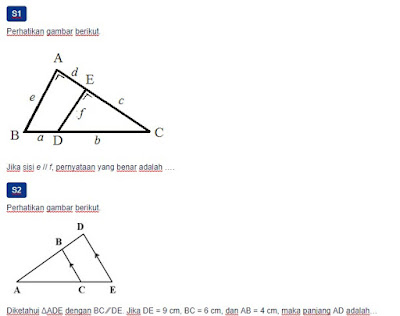
S1

Perhatikan gambar berikut.

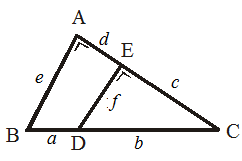
Jika sisi e // f, pernyataan yang benar adalah ….

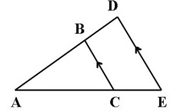
S2

Perhatikan gambar berikut.

Diketahui ΔADE dengan BC ⁄⁄ DE. Jika DE = 9 cm, BC = 6 cm, dan AB = 4 cm, maka panjang AD adalah…

S3

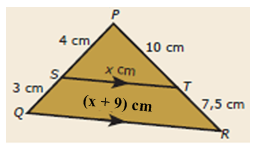
Berdasarkan gambar berikut, panjang EF adalah …

S4

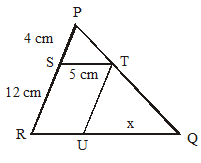
Perhatikan gambar di bawah ini. Jika panjang SR = TU, maka panjang x adalah ....

S5

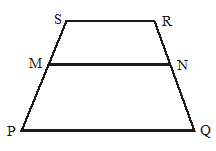
Perhatikan gambar berikut ini.

Diketahui trapesium PQRS dengan PQ//MN. Jika panjang SM = 5 cm, MP =4 cm, dan RQ = 13,5 cm, maka panjang RN = ….

S6

Perhatikan gambar berikut.

Jika panjang sisi AB = 12 cm dan BD = 7,2 cm, maka panjang sisi AC adalah ....

S7

Perhatikan gambar berikut.

Keliling ΔPQR adalah .…

S8

Perhatikan gambar ΔABC dibawah ini.

Jika panjang BD = 24 cm dan AD = 16 cm, maka luas ΔABC adalah ....

S9

Perhatikan gambar dibawah ini.

Diketahui panjang SR = 9 cm, RN= 6 cm, NQ = 8 cm, dan luas trapesium PQRS = 192 cm2 . Jika tinggi trapesium = 12 cm, maka panjang sisi MN adalah ....

S10

Perhatikan gambar dibawah ini.

Luas persegipanjang pada gambar adalah ....

Share this post