Contoh Soal Penggunaan Teorema Sisa pada Pembagi Bentuk Kuadrat
Contoh Soal Penggunaan Teorema Sisa pada Pembagi Bentuk Kuadrat - Pada topik sebelumnya, kalian telah mempelajari Teorema Sisa pada pembagian suku banyak oleh bentuk linear yaitu (x - k ) dan (ax - b ). Dari pembelajaran tersebut, kalian tentu sudah sangat memahami Teorema Sisa I dan Teorema Sisa II. Nah, pada pembelajaran kali ini kita akan coba untuk mencari sisa pembagian suku banyak dengan suku banyak lain yang berderajat dua (ax2 + bx + c ). Namun untuk menyederhanakan pembahasan, kita gunakan
a = 1 dan bentuk (ax2 + bx + c ) dapat difaktorkan menjadi (x - j ) (x - k ) dimana j, k ∈ R.
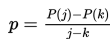
a = 1 dan bentuk (ax2 + bx + c ) dapat difaktorkan menjadi (x - j ) (x - k ) dimana j, k ∈ R.
Pembagian Suku Banyak oleh (x - j ) (x - k )
Suatu suku banyak P (x) yang dibagi oleh (x - j ) (x - k ) dapat kita tulis sebagai berikut.
P (x ) = (x - j ) (x - k ) H (x ) + s (x )
dengan H (x ) sebagai hasil pembagian dan s (x ) merupakan sisa pembagian.
Perlu kalian pahami bahwa sisa pembagian s (x ) tidak mungkin memiliki derajat lebih dari satu. Dengan kata lain s (x ) hanya dapat berbentuk px + q dengan p, q ∈ R. Hal ini sama dengan pembagian bilangan pada umumnya, sisa pembagian pasti lebih kecil dari pembaginya. Misalnya pembagian bilangan dengan 5, maka sisa yang mungkin pastilah 0, 1, 2, 3, atau 4. Prinsip dari sisa pembagian pada bilangan ini juga berlaku pada sisa pembagian suku banyak.
Sekarang coba perhatikan bahwa terdapat dua pembuat nol dari pembagi (x - j ) (x - k ) yaitu x = j dan x = k. Nilai suku banyak pada kedua pembuat nol ini memungkinkan kita untuk menentukan sisa pembagian yang dimaksud tanpa harus menggunakan dua metode yang kalian pelajari sebelumnya. Perhatikan penjabaran berikut.
Saat x = j dan s (x ) = px + q maka
P (x ) = (x - j ) (x - k ) H (x ) + s (x )
P (j ) = (j - j ) (j - k ) H (j ) + (pj + q )
P (j ) = (0) (j - k ) H (j ) + (pj + q )
P (j ) = pj + q ... (1)
Saat x = k dan s (x ) = px + q maka
P (x ) = (x - j ) (x - k ) H (x ) + s (x )
P (k ) = (k - j ) (k - k ) H (k ) + (pk + q )
P (k ) = (k - j ) (0) H (k ) + (pk + q )
P (k ) = pk + q ... (2)
Oleh karena nilai dari j, k, P (j ), P (k ) diketahui, maka kita dapat menentukan sisa pembagian
s (x ) = px + q dengan mencari nilai dari p dan q. Dengan menerapkan metode eliminasi pada persamaan (1) dan (2), diperoleh :
s (x ) = px + q dengan mencari nilai dari p dan q. Dengan menerapkan metode eliminasi pada persamaan (1) dan (2), diperoleh :
pj + q = P (j )
pk + q = P (k ) _
pj - pk = P (j ) - P (k )
p (j - k ) = P (j ) - P (k )
dengan demikian, didapatkan nilai p yaitu,
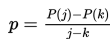
SOAL 1
Suku banyak berderajat n > 2 yang dibagi dengan suku banyak lain berderajat 2 akan memberikan sisa berupa ....
SOAL 2
Suatu suku banyak dinyatakan dalam pembagi, hasil bagi dan sisa bagi sebagai berikut.
P (x ) = (x - j ) (x - k ) H (x ) + s (x )
nilai suku banyak tersebut akan sama dengan sisa pembagiannya jika nilai x = ....
SOAL 3
Sisa pembagian suku banyak
P (x) = x5 - 3x4 + 2x3 + x2 - 2x + 7
oleh (x - 1)(x - 2) adalah ....
SOAL 4
Sisa pembagian suku banyak P (x) = x4 - 2x2 + 3x + 1
oleh (x2 - 1) adalah ....
SOAL 5
Suku banyak P (x) bersisa 15 saat dibagi oleh (x - 1), dan bersisa 5 saat dibagi (x + 4). Sisa pembagian suku banyak P (x) oleh x2 + 3x - 4 adalah ....
SOAL 6
Suku banyak P (x) = x5 + 2x4 + x3 + 2x2 + x + 2 memberikan sisa berupa Ax + B apabila dibagi oleh x2 + 3x + 2. Nilai dari A x B adalah ....
SOAL 7
Sisa pembagian suku banyak P (x) = 36x4 - 6x3 + x +
oleh 6x2 - 5x + 1 adalah ....
SOAL 8
Suku banyak P (x) bersisa 5x + 1 saat dibagi dengan x2 - 1 dan bersisa -3x - 2 saat dibagi x2 - 4. Sisa dari P (x ) saat dibagi oleh x2 + x - 2 adalah ....
SOAL 9
Suku banyak P (x) = x4 + Ax3 + Bx2 + 2x - 1 habis saat
dibagi oleh x2 - 2x - 3. Nilai dari A - B adalah ....
SOAL 10
Pembagian suku banyak P (x) berderajat lebih dari 2 oleh (x - a)(x - b) untuk a, b ∈ R memberikan sisa berupa
s (x) = px + q dimana P (a) = ap + q dan P (b) = bp + q. Pernyataan yang benar mengenai nilai p dan q adalah ....
s (x) = px + q dimana P (a) = ap + q dan P (b) = bp + q. Pernyataan yang benar mengenai nilai p dan q adalah ....
