Transformasi Geometri Dilatasi
Transformasi Geometri Dilatasi - Pada topik ini, kita akan mempelajari transformasi dilatasi. Transformasi dilatasi (perkalian) adalah transformasi yang mengubah ukuran (memperbesar atau memperkecil) suatu bangun namun tidak mengubah bentuk bangun tersebut.
Sebuah dilatasi berpusat di titik O(0,0) dengan faktor skala k dinotasikan oleh [O, k].
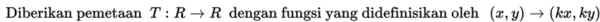
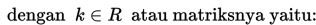
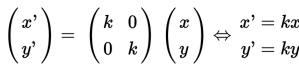
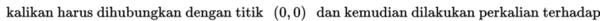
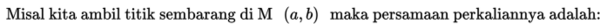
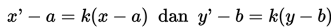
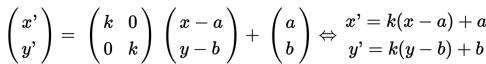
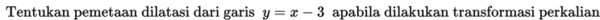
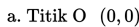
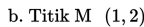
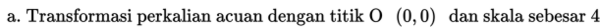
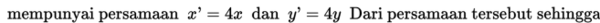
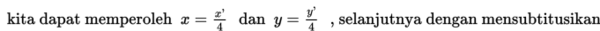
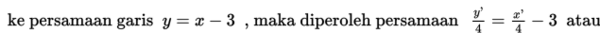
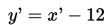
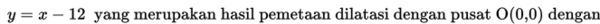
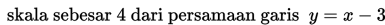
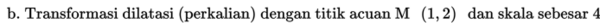
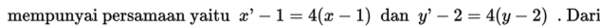
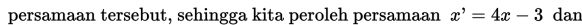
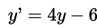
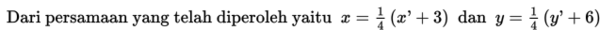
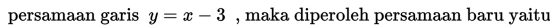

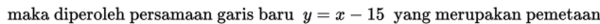
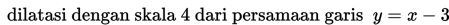
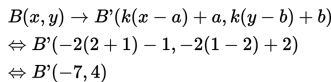
 |
| Transformasi Geometri Dilatasi |
Sebuah dilatasi berpusat di titik O(0,0) dengan faktor skala k dinotasikan oleh [O, k].
Kita dapat mendefinisikan transformasi dilatasi sebagai berikut:
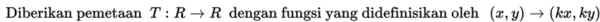
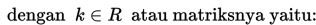
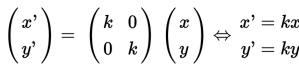
panjang garis tersebut.
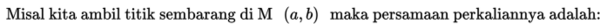
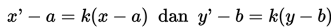
Dilatasi yang berpusat di P(a, b) dengan faktor skala k dinotasikan dengan [P(a, b), k]
Maka diperolah matriksnya yaitu:
Maka diperolah matriksnya yaitu:
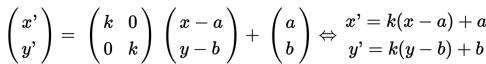
Untuk lebih jelasnya, mari kta perhatikan contoh berikut:
Contoh 1.
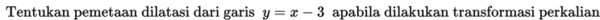
dengan skala sebesar 4 dengan acuan
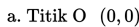
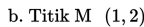
Penyelesaian:
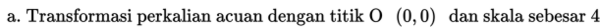
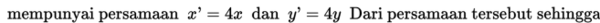
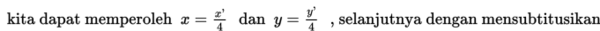
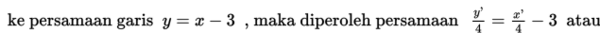
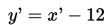
Dengan menghapus tanda “aksen”, maka diperoleh persamaan garis baru yaitu
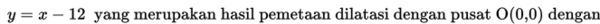
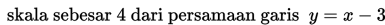
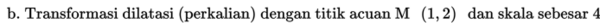
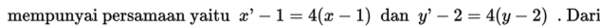
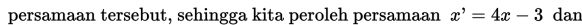
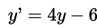
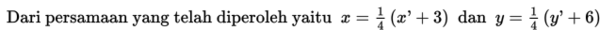
selanjutnya dengan mensubtitusikan persamaan yang telah diperoleh yaitu ke
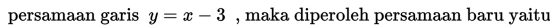

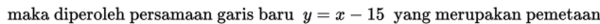
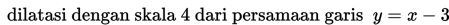
Contoh 2.
Tentukan bayangan titik B(2, 1) dengan pusat P(-1, 2) dengan skala sebesar -2 atau dapat dinotasikan dengan dilatasi oleh [P(-1, 2), -2].
Tentukan bayangan titik B(2, 1) dengan pusat P(-1, 2) dengan skala sebesar -2 atau dapat dinotasikan dengan dilatasi oleh [P(-1, 2), -2].
Penyelesaian:
Karena titik B(2, 1) dilatasi dengan pusat P(-1. 2) dan skala sebesar -2, sehingga dapat kita peroleh hasil perkalian (dilatasi) sebagai berikut:
Karena titik B(2, 1) dilatasi dengan pusat P(-1. 2) dan skala sebesar -2, sehingga dapat kita peroleh hasil perkalian (dilatasi) sebagai berikut:
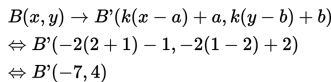
Jadi, bayangan dari koordinat titik B(2, 1) adalah B’ dengan koordinat (-7, 4) atau B’(-7, 4).