Periodesitas Fungsi Trigonometri

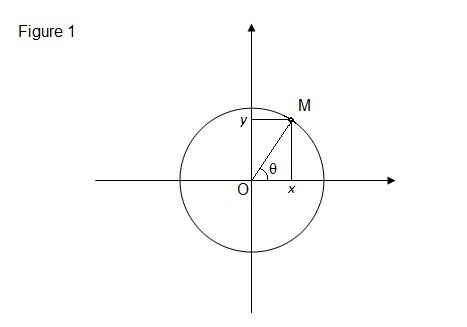
Periodesitas Fungsi Trigonometri -Ketika kita mendefinisikan identitas fungsi trigonometri dalam sebuah lingkaran, kita akan menggunakan relasi : 

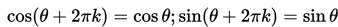
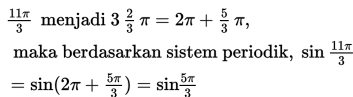
Periodesitas Fungsi Trigonometri

Karena sudut θ dan θ+2pi terletak pada titik yang sama, yaitu M, maka nilai sinus dan cosinus untuk kedua sudut tersebut adalah sama. 

cos(θ+2π)=cosθ;sin(θ+2π)=sinθ$\cos (\theta +2\pi )=\cos \theta ;\sin (\theta +2\pi )=\sin \theta$

Selanjutnya, karena grafik sin θ dan cos θ bersifat periodik dengan periode 2pi, maka : 

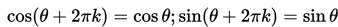
Contoh 1.

Sederhanakanlah  

sin11π3$\sin \frac{11\pi }{3}$ menjadi bentuk lain, dimana argumennya terletak pada interval [0,2pi]!

Penyelesaian :

Dengan mengubah bentuk pecahan

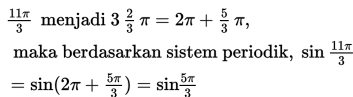
Contoh 2.

Sederhanakanlah cos (426o) menjadi bentuk lain dimana argumennya terletak pada interval [0,360o]!

Penyelesaian :

Seperti pada contoh 1, kita akan mengubah 426o menjadi penjumlahan antara dua sudut sebagai berikut :  426o=360o+66o. Dengan demikian, cos (426o)=cos (66o).

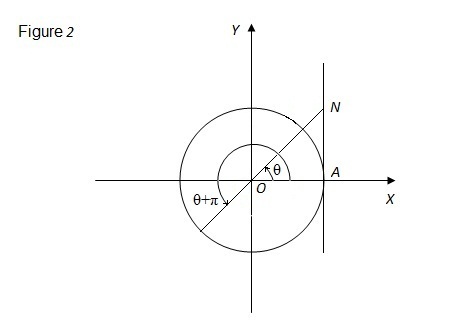
Selanjutnya, dari gambar di bawah ini, diketahui bahwa : tanθ sama dengan nilai ordinat dari titik N yang terletak pada sumbu AN pada suatu lingkaran. 

Dengan demikian, sudut θ+pi juga terletak pada titik yang sama dalam sumbu tangen. Oleh karena itu, tan(θ+pi)=tan(θ). Selanjutnya, karena cot θ =1/tan θ, maka cot (θ+pi)=cot (θ).

Contoh 3.

Sederhanakanlah  

tan11π3+3cot15π6 menjadi bentuk lain dimana argumennya terletak pada interval [0,pi]!$\mathrm{<br>}$

$\tan \frac{11\pi }{3}+3\cot \frac{15\pi }{6}\text{ menjadi bentuk lain dimana argumennya terletak pada interval }\left[\mathrm{0,}pi\right]!$

Penyelesaian :

Dengan menyederhanakan semua bentuk pecahan, maka diperoleh : 

11π3=3π+2π3 dan 15π6=2π+3π6.Karena sifat periodik, maka cot15π6=cot3π6=cotπ2 dan tan11π3=tan(2π3).Dengan demikian, tan11π3+3cot15π6=tan2π3+3cotπ2.
$\begin{array}{l}\frac{1}{}\end{array}$

$\begin{array}{l}\frac{1\pi }{3}=3\pi +\frac{2\pi }{3}\text{ dan }\frac{15\pi }{6}=2\pi +\frac{3\pi }{6}.\\ \text{Karena sifat periodik}\text{, }\end{array}$

$\begin{array}{l}\text{maka }\cot \frac{15\pi }{6}=\cot \frac{3\pi }{6}=\cot \frac{\pi }{2}\text{ dan }\tan \frac{11\pi }{3}=\tan (\frac{2\pi }{3}).\end{array}$

$\begin{array}{l}\text{Dengan demikian}\text{, }\tan \frac{11\pi }{3}+3\cot \frac{15\pi }{6}=\tan \frac{2\pi }{3}+3\cot \frac{\pi }{2}.\end{array}$

Catatan :

Menyederhanakan bentuk trigonometri seperti pada contoh di atas, akan membantu kita dalam menghitung nilai dari suatu fungsi trigonometri.

Share this post