Menggunakan sin²(θ) + cos²(θ) = 1 Dalam Subtitusi Trigonometri
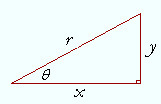
Menggunakan sin²(θ) + cos²(θ) = 1 Dalam Subtitusi Trigonometri - Berdasarkan theorema Pythagoras,
PENYELESAIAN :
Dengan menggunakan identitas trigonometri : cos(π/2 - θ) = sin θ, diperoleh :
 |
| Menggunakan sin²(θ) + cos²(θ) = 1 Dalam Subtitusi Trigonometri |
x² + y² = r²
dimana x dan y adalah sisi-sisi segitiga siku-siku dan r adalah sisi miring (hipotenusa) dari segitiga tersebut.

Selanjutnya, dengan membagi kedua ruas persamaan di atas dengan r², diperoleh hasil sebagai berikut :
x2/r2 + y2/r2 = r2/r2 = 1
Ternyata hasil yang diperoleh sesuai dengan definisi dalam trigonometri, yaitu :
cos²θ + sin²θ = 1
OR sin²θ + cos²θ = 1
Dalam pelajaran ini, kalian akan belajar tentang bagaimana menggunakan identitas trigonometri tersebut dalam menyelesaikan beberapa permasalahan.
Berikut ini adalah beberapa contoh yang akan membantu meningkatkan pemahaman kalian.
CONTOH 1 :
Sederhanakanlah bentuk berikut ini : cos² θ + cos²(π/2 - θ)
Dengan menggunakan identitas trigonometri : cos(π/2 - θ) = sin θ, diperoleh :
cos² θ + cos²(π/2 - θ) = cos² θ + sin2 θ = 1
CONTOH 2:
Apakah persamaan berikut ini bernilai benar?
(sin x)/(1-cos x) = (1+cos x)/sin x
PENYELESAIAN :
Dengan mengalikan ruas kiri persamaan dengan konjugatnya (bilangan sekawan), maka diperoleh :
(sin x)/(1-cos x) = (sin x)/(1-cosx) x (1+cos x)/(1+cos x)
= (sin x)(1+cos x)/(1-cos² x)
= (sin x)(1+cos x)/(1-cos² x)
= (sin x)(1+cos x)/sin² x (Note : sin²(θ) + cos²(θ) = 1)
= (1+cos x)/sin x
Karena hasil yang diperoleh sama dengan ruas kanan dari persamaan di atas, maka persamaan di atas bernilai benar.
CONTOH 3 :
Dari pilihan berikut ini, manakah yang merupakan bentuk sederhana dari : 4x - cos4x?
A) sin2x + cos2x
B) 1
C) sin2x - cos2x
D) Tidak ada jawaban yang benar
PENYELESAIAN :
sin4x - cos4x = (sin2x - cos2x) (sin2x + cos2x)
= (sin2x - cos2x) (1)
= (sin2x - cos2x)
Dengan demikian, opsi C adalah jawaban yang benar.