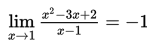Arti Limit Fungsi Aljabar di Suatu Titik
Arti Limit Fungsi Aljabar di Suatu Titik - Konsep limit merupakan dasar atau landasan utama untuk mempelajari deferensial dan integral dari kalkulus yang merupakan salah satu cabang matematika. Kalkulus suatu alat yang banyak digunakan pada bidang teknik, bisnis dan ekonomi, ilmu pengetahuan alam dan bidang-bidang lain yang permasalahannya melibatkan peubah-peubah kontinu.
Adapun perkiraan tinggi benturan dikatakan sebagai limit fungsi f(x) untuk x mendekati c dari arah kiri dan ditulis :
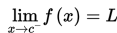
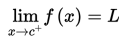
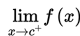
Contoh

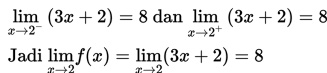
Definisi Limit Fungsi
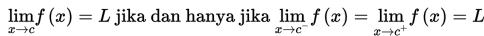
Contoh
Selidikilah nilai
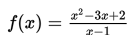
Penyelesaian :
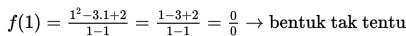
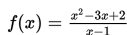
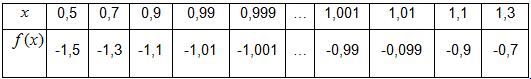
Nilai limit
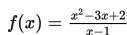
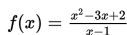
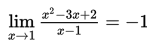
 |
| Arti Limit Fungsi Aljabar di Suatu Titik |
Coba kita bayangkan apabila seorang anak melempar sebuah bola karet ke dinding kaca. Perjalanan bola ini terus menerus akan mendekati dinding kaca atau jarak bola dengan dinding kaca semakin dekat atau semakin kecil, seperti terlihat pada gambar berikut :

Gerakan bola tersebut akan membentur diding kaca dan kita diharapkan bisa menentukan ketinggian bola saat membentur dinding kaca.
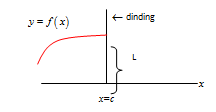
Dalam kalkulus, jejak bola ini dapat kita ilustrasikan sebagai : grafik fungsi y = f(x) untuk x < c dan dinding kaca sebagai garis tegak x = c
Adapun perkiraan tinggi benturan dikatakan sebagai limit fungsi f(x) untuk x mendekati c dari arah kiri dan ditulis :
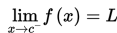
Dalam situasi tertentu karena ada gangguan yang menyebabkan beberapa bola tidak dapat bergerak mendekati dinding kaca mungkin akan menjauh pada ketinggian yang bisa terukur. Dalam hal ini dikatakan tidak ada nilai limit fungsi f(x) untuk x mendekati c dari arah kiri.
Selanjutnya, untuk gerakan bola dari arah sebelah kanan, jika digunakan penalaran yang sama maka perkiraan tinggi bola adalah limit fungsi f(x) untuk x mendekati c dari arah kanan dan ditulis :
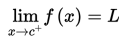
Jika tinggi benturan bola dari arah kanan tidak dapat diperkirakan, maka
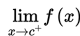
tidak ada.
Limit selalu berhubungan dengan suatu fungsi, baik fungsi aljabar maupun fungsi trigonometri. Pada pembahasan berikut kalian akan terlebih dahulu mempelajari limit fungsi aljabar.
Contoh
Diberikan fungsi f(x) = 3x + 2, yang terdefinisi untuk semua nilai x bilangan nyata.
Nilai-nilai fungsi f(x) untuk nilai untuk x mendekati 2 adalah sebagai berikut :
Nilai-nilai fungsi f(x) untuk nilai untuk x mendekati 2 adalah sebagai berikut :

Berdasarkan tabel di atas, semakin x dekat dengan 2 dari arah kiri maka nilai f(x) mendekati nilai 8 dan semakin x dekat dengan 2 dari arah kanan maka nilai f(x) mendekati nilai 8. Dengan demikian, dapat disimpulkan bahwa limit f(x) untuk x mendekati 2 sama dengan 8 :
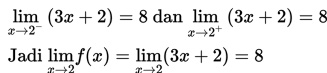
Definisi Limit Fungsi
Jika suatu fungsi y = f(x) didefinisikan untuk x sekitar c, maka
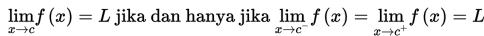
Contoh
Selidikilah nilai
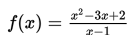
untuk x mendekati 1
Penyelesaian :
1. Untuk x = 1 maka
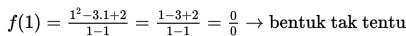
2. Untuk x mendekati 1 , nilai dari
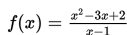
dapat diperoleh dengan membuat tabel dari nilai-nilai yang dekat dengan 1 yaitu lebih dari 1 dan kurang dari 1.
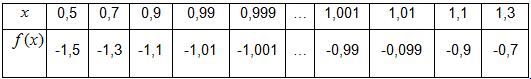
Nilai limit
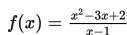
untuk x mendekati 1 dari arah kiri nilai f(x) mendekati –1 dan untuk x mendekati 1 dari arah kanan nilai f(x) mendekati –1 . Oleh karena itu nilai limit
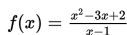
untuk x mendekati 1 adalah –1 dan dapat ditulis