Sifat-sifat Fungsi Trigonometri

Sifat-sifat Fungsi Trigonometri - Anda telah mengetahui bahwa sin x dan cos x adalah fungsi periodik dengan periode 2π. Ini mengimplikasikan sin (x+2π)=sin x, cos (x+2π)= cos x untuk setiap real x. 

Sifat-sifat Fungsi Trigonometri

Tetapi jika kita ingin mentransformasikan ekspresi sin (2π-x) atau cos (2π-x) kita seharusnya menambah ide lain --simetri. Yaitu,

sin (2π-x)=sin (-x)=-sin x; cos(2π-x)=cos (-x)=cos x.

Cara yang serupa dengan tangen:

tan (2π-x)=tan (-x)=-tan x.

Selain itu, penyebab π periode tangen kita juga mempunyai

tan (π+x)=tan x; tan (π-x)=tan(-x)=-tan(x).

Komentar 1.

Karakteristik ini masih ada jika kita menggantikan 2π dengan 2πk untuk sinus dan cosinus dan jika kita menggantikan π dengan πk untuk setiap integer k.

Contoh 1.

Kurangi ekspresi pada argumen fungsi x: f(x)=

sin(8π−x)+3cos(10π−3x)tg(7π−2x)$$\frac{sin\left(8\pi -x\right)+3\cos (10\pi -3x)}{tg(7\pi -2x)}$$

Solusi

Dikarenakan karakteristik yang disebutkan di atas kita mempunyai sin(8π-x)=sin(4*2π-x)=-sin x; cos (10π-3x)=cos(5*2 π-3x)=cos(3x); tg (7π-2x)=tg(7*π-2x)=-tg(2x). Jadi,

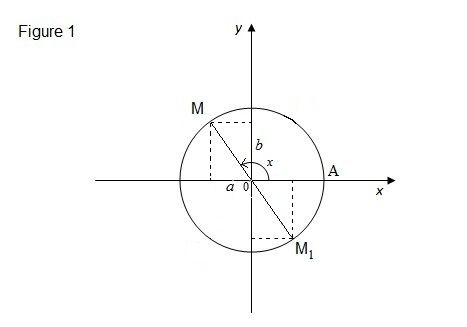
Mari kita kembali ke unit lingkaran dan mempertimbangkan dua sudut: 

x=∠AOM$x=\angle AOM$ and π+x=∠AOM1$\pi +x=\angle AO{M}_1$ (lihat gambar1)

Jika M mempunyai koordinat a dan b, maka M1 mempunyai koordinat (-a) dan (-b).Karena definisi,

sin x=b, cos x=a; sin (π+x)=-b, cos (π+x)=-a.

Karenanya, sin (π+x)=-sin x; cos (π+x)=-cos x.

Menggunakan formula ini dengan simetri sinus dan cosinus, satu yang dapat disimpulkan

sin (π-x)=-sin(-x)=sin x; cos (π-x)=-cos(-x)=-cos x.

Komentar 2.

Ukuran sudut, menggambarkan karakteristik fungsi trigonometri, dapat sama radian seperti derajat.

Contoh 2.

Kurangi ekspresi fungsi sudut yang dimiliki kuadran pertama: sin (310o).

Solusi

Mari mempresentasikan 310o dalam bentuk 360o-50o, maka sin(310o)= sin(360o-50o)=sin(-50o)=- sin(50o).

Share this post