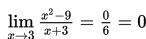Teorema Dasar Limit
Teorema Dasar Limit - Setelah mempelajari tentang pengertian limit, selanjutnya kalian akan mempelajari sifat-sifat dan teorema dasar limit.
Mari kita perhatikan beberapa contoh berikut.
Contoh 1
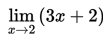
Cara 1 : Menggunakan Tabel

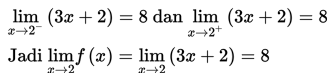
Cara 2 :
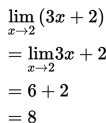
Contoh 2
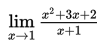
Cara 1 : Menggunakan Tabel
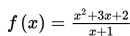

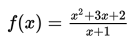
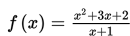
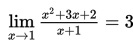
Cara 2 :
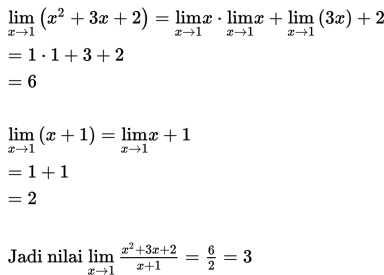

Contoh :
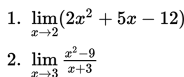
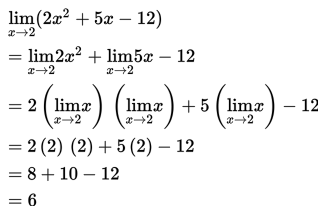
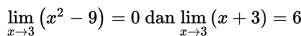
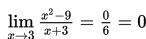
 |
| Teorema Dasar Limit |
Mari kita perhatikan beberapa contoh berikut.
Contoh 1
Hitung nilai
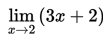
Cara 1 : Menggunakan Tabel

Berdasarkan tabel di atas, apabila nilai x semakin dekat dengan 2 dari arah kiri maka nilai f(x) hampir mendekati nilai 8 dari arah kiri dan apabila nilai x semakin dekat dengan 2 dari arah kanan maka nilai f(x) hampir mendekati nilai 8 dari arah kanan.
Dengan demikian, dapat disimpulkan bahwa limit f(x) mendekati 2 sama dengan 8 dan dapat ditulis sebagai berikut :
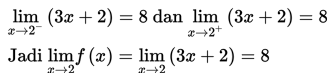
Cara 2 :
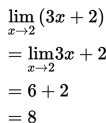
Contoh 2
Hitung nilai
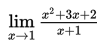
Cara 1 : Menggunakan Tabel
Untuk x mendekati 1, nilai limit dari
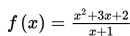
dapat diperoleh dengan cara membuat tabel dari nilai-nilai yang dekat dengan 1 yaitu lebih atau kurang dari 1.

Nilai limit
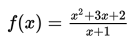
untuk x mendekati 1 dari arah kiri mendekati 3 dan untuk x mendekati 1 dari arah kanan nilai f(x) mendekati 3. Oleh karena itu nilai limit
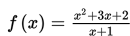
untuk x mendekati 1 adalah 3 dan dapat ditulis
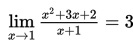
Cara 2 :
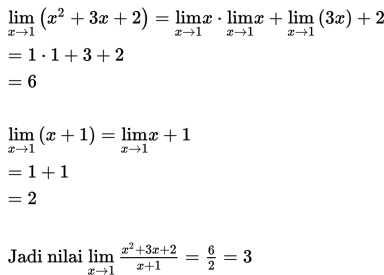
Dengan melalui contoh di atas, berikut ini adalah teorema dasar limit.

Contoh :
Hitunglah limit berikut :
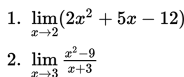
Penyelesaian :
Dengan menggunakan teorema di atas, maka langkah penyelesaiannya sebagai berikut :
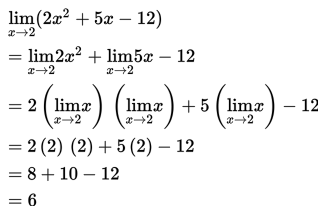
- Dengan cara seperti di atas maka diperoleh
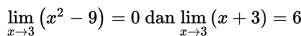
Kemudian dengan menggunakan teorema 2c diperoleh :