Contoh Soal Konsep sistem pertidaksamaan kuadrat dua variabel
Contoh Soal Konsep sistem pertidaksamaan kuadrat dua variabel - Pada topik sebelumnya, kalian telah mempelajari sistem persamaan kuadrat dua variabel. Apakah kalian masih ingat tentang materi tersebut? Mari kita ulang sebentar materi tersebut dengan menyelesaikan masalah berikut.
Seorang polisi bertugas memonitor kecepatan kendaraan yang melalui suatu jalan. Tiba-tiba seorang pengendara sepeda motor melaju dengan kecepatan tetap melewati mobil patroli. Polisi yang bertugas, melihat ke arah alat monitor kecepatan dan memperoleh informasi bahwa kecepatan motor tersebut adalah 30 m/s. Polisi yang semula dalam keadaan diam kemudian mengejar pengendara motor dengan percepatan tetap sebesar 5 m/s2. Kapan mobil polisi dapat menyalip motor tersebut?
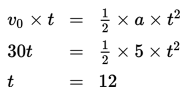
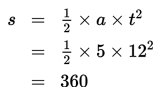
Sekarang mari kita ingat kembali tentang bentuk umum persamaan kuadrat dua variabel yang pernah kalian pelajari. Masih ingatkah kalian tentang hal tersebut?
Persamaan kuadrat dua variabel mempunyai bentuk umum :
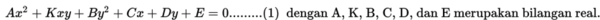
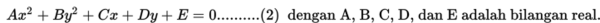
Selanjutnya mari kita pelajari topik ini, yaitu tentang sistem pertidaksamaan kuadrat dua variabel. Sistem pertidaksamaan kuadrat dua variabel merupakan kumpulan beberapa pertidaksamaan yang memuat paling sedikit satu pertidaksamaan kuadrat dua variabel. Penyelesaian dari sistem pertidaksamaan kuadrat dua variabel merupakan perpotongan atau irisan dari beberapa pertidaksamaan yang membentuk sistem tersebut. Adapun grafik daerah himpunan penyelesaian dibatasi oleh kurva yang membentuk sistem pertidaksamaan kuadrat dua variabel. Selanjutnya pertidaksamaan yang memuat , kurva pembatas digambar dengan menggunakan garis putus, sedangkan pertidaksamaan yang memuat ≤ atau ≥ , kurva pembatas digambar menggunakan garis utuh. Untuk lebih jelasnya mari kita mencermati contoh di bawah ini.
Contoh 1 :
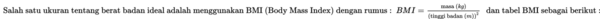

Penyelesaian :
155 cm = 1,55 m
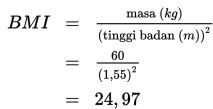
Masalah tersebut merupakan salah satu penerapan tentang pertidaksamaan kuadrat dua variabel. Selanjutnya kita akan mempelajari masalah tentang sistem pertidaksamaan kuadrat dua variabel berikut.
Contoh 2 :
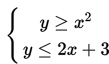
Penyelesaian :
Untuk menyelesaikan sistem pertidaksamaan di atas, ada beberapa langkah yang harus di tempuh.

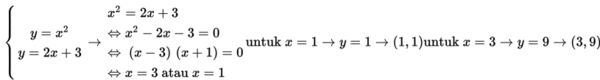
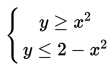
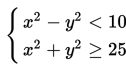
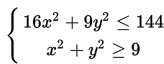

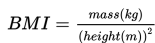
Seorang polisi bertugas memonitor kecepatan kendaraan yang melalui suatu jalan. Tiba-tiba seorang pengendara sepeda motor melaju dengan kecepatan tetap melewati mobil patroli. Polisi yang bertugas, melihat ke arah alat monitor kecepatan dan memperoleh informasi bahwa kecepatan motor tersebut adalah 30 m/s. Polisi yang semula dalam keadaan diam kemudian mengejar pengendara motor dengan percepatan tetap sebesar 5 m/s2. Kapan mobil polisi dapat menyalip motor tersebut?
Penyelesaian :
Mobil patroli akan dapat menyalip motor apabila jarak yang ditempuh oleh kedua kendaraan sama. Dengan kata lain,
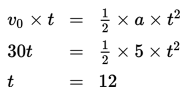
Jadi, setelah 12 detik mobil patroli baru dapat menyalip motor.
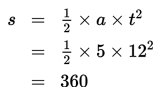
Jarak yang diperlukan untuk menyalip motor dari posisi semula adalah 360 meter.
Sekarang mari kita ingat kembali tentang bentuk umum persamaan kuadrat dua variabel yang pernah kalian pelajari. Masih ingatkah kalian tentang hal tersebut?
Persamaan kuadrat dua variabel mempunyai bentuk umum :
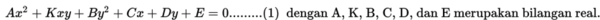
Apabila kalian ingin mengetahui grafiknya, pelajarilah informasi berikut.
1) Jika K = 0 dan A = B ≠ 0, kurva berbentuk lingkaran
2) Jika K2 – 4AB = 0, kurva berbentuk parabola
3) Jika K2 – 4AB < 0, kurva berbentuk elips
4) Jika K2 – 4AB > 0, kurva berbentuk hiperbola
2) Jika K2 – 4AB = 0, kurva berbentuk parabola
3) Jika K2 – 4AB < 0, kurva berbentuk elips
4) Jika K2 – 4AB > 0, kurva berbentuk hiperbola
Selanjutnya, jika nilai K = 0, maka bentuk Ax2 + Kxy +By2 + Cx + Dy + E = 0 menjadi :
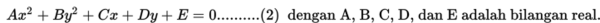
Mari kita cermati persamaan (2).
1) Jika A = 0 atau B = 0 tetapi tidak bersamaan sama dengan nol, kurva berbentuk parabola
2) Jika A = B ≠ 0, kurva berbentuk lingkaran
3) Jika A ≠ B dan bertanda sama, kurva berbentuk elips
4) Jika A ≠ B dan berlawanan tanda, kurva berbentuk hiperbola
2) Jika A = B ≠ 0, kurva berbentuk lingkaran
3) Jika A ≠ B dan bertanda sama, kurva berbentuk elips
4) Jika A ≠ B dan berlawanan tanda, kurva berbentuk hiperbola
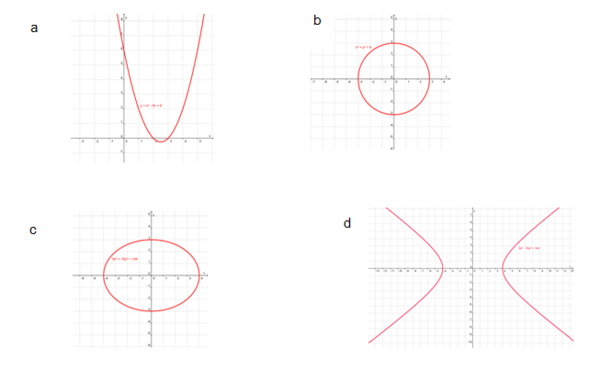
Berikut ini adalah contoh grafik persamaan kuadrat dua variabel.

- Gambar a adalah parabola dengan persamaan y = x2 – 5x + 6
- Gambar b adalah lingkaran dengan persamaan x2 + y2 = 9
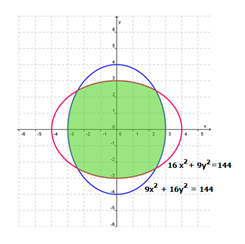
- Gambar c adalah elips dengan persamaan 9x2 + 16y2 = 144
- Gambar d adalah hiperbola dengan persamaan 9x2 – 16y2 = 144
Selanjutnya mari kita pelajari topik ini, yaitu tentang sistem pertidaksamaan kuadrat dua variabel. Sistem pertidaksamaan kuadrat dua variabel merupakan kumpulan beberapa pertidaksamaan yang memuat paling sedikit satu pertidaksamaan kuadrat dua variabel. Penyelesaian dari sistem pertidaksamaan kuadrat dua variabel merupakan perpotongan atau irisan dari beberapa pertidaksamaan yang membentuk sistem tersebut. Adapun grafik daerah himpunan penyelesaian dibatasi oleh kurva yang membentuk sistem pertidaksamaan kuadrat dua variabel. Selanjutnya pertidaksamaan yang memuat , kurva pembatas digambar dengan menggunakan garis putus, sedangkan pertidaksamaan yang memuat ≤ atau ≥ , kurva pembatas digambar menggunakan garis utuh. Untuk lebih jelasnya mari kita mencermati contoh di bawah ini.
Contoh 1 :
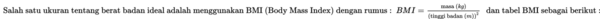

Ida mempunyai tinggi badan 155 cm dan berat badan 60 kg. Teman-teman Ida mengatakan bahwa Ida kegemukan. Apabila menggunakan BMI, apakah pernyataan tersebut benar?
Penyelesaian :
155 cm = 1,55 m
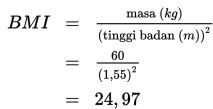
Berdasarkan hasil perhitungan di atas, nilai BMI Ida terletak pada kategori berat badan ideal 18,5 ≤ 24,97 ≤ 25. Dengan kata lain, pernyataan mengenai Ida kegemukan adalah salah.
Masalah tersebut merupakan salah satu penerapan tentang pertidaksamaan kuadrat dua variabel. Selanjutnya kita akan mempelajari masalah tentang sistem pertidaksamaan kuadrat dua variabel berikut.
Contoh 2 :
Tentukan daerah himpunan penyelesaian dari sistem pertidaksamaan :
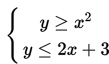
Penyelesaian :
Untuk menyelesaikan sistem pertidaksamaan di atas, ada beberapa langkah yang harus di tempuh.
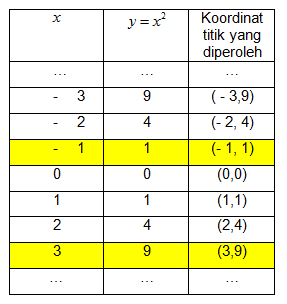
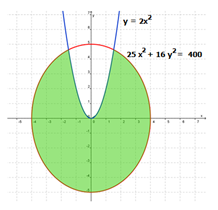
(1) Buat kurva pembatas, yaitu y = x2 (parabola) dengan cara membuat tabel.

Ambil sebarang titik yang tidak terletak pada kurva sebagai titik uji, kemudian substitusikan ke persamaan kurva.
Sebagai contoh, kita akan uji titik (1,2).
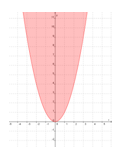
(1,2) → x = 1 dan y = 2 → x2 = 1 dan 2 > 1 → y > x2 sehingga daerah yang memenuhi y > x2 adalah daerah di dalam kurva.
(1,2) → x = 1 dan y = 2 → x2 = 1 dan 2 > 1 → y > x2 sehingga daerah yang memenuhi y > x2 adalah daerah di dalam kurva.
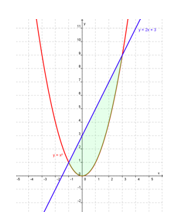
Dengan demikian,, gambar daerah himpunan penyelesaian y ≥ x2 sebagai berikut.

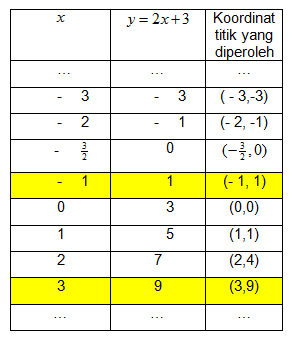
(2) Buat garis pembatas, yaitu y = 2x + 3 (garis lurus) dengan cara membuat tabel.

Perlu diketahui bahwa pada saat membuat grafik berupa garis, kalian cukup mencari dua titik yang terletak pada garis tersebut, misalkan :

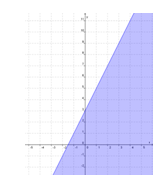
Langkah berikutnya adalah mengambil sebarang titik yang tidak terletak pada garis sebagai titik uji, misalkan titik (0,0) kemudian pada persamaan garis y = 2x + 3 kita substitusikan x = 0 dan y = 0. Oleh karena diperoleh hasil 0 < 3 , maka daerah yang memenuhi y ≤ 2x + 3 adalah daerah di bawah garis.
Gambar daerah himpunan penyelesaian y ≤ 2x + 3 sebagai berikut.

(3) Tentukan irisan dua daerah himpunan penyelesaian tersebut.

Perhatikan bahwa titik (-1,1) dan (3,9) merupakan titik potong kedua kurva. Hal ini berarti bahwa titik (-1,1) dan (3,9) terletak pada parabola maupun pada garis (lihat baris yang berwarna kuning pada tabel).
Koordinat titik potong kedua kurva juga dapat ditentukan dengan cara menyelesaikan sistem persamaan :
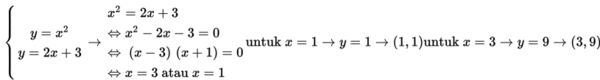
S1
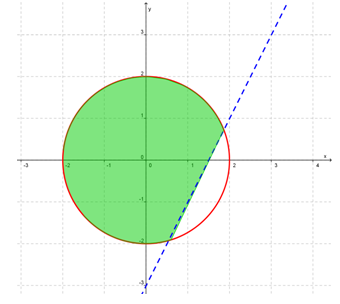
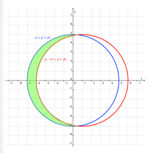
Daerah yang diarsir pada gambar berikut merupakan daerah himpunan penyelesaian dari suatu SPtKDV.

SPtKDV tersebut adalah ….
S2
Perhatikan SPtKDV berikut.
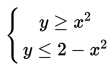
Gambar yang tepat untuk daerah himpunan penyelesaian SPtKDV tersebut adalah ….
S3
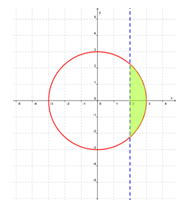
Perhatikan gambar berikut ini.

Daerah yang diarsir menyatakan daerah himpunan penyelesaian suatu sistem pertidaksamaan kuadrat dua variabel. Sistem pertidaksamaan yang sesuai untuk gambar tersebut adalah ….
S4
Perhatikan gambar berikut.

Daerah yang diarsir merupakan daerah himpunan penyelesaian sistem pertidaksamaan ….
S5
Perhatikan gambar berikut.

Sistem pertidaksamaan yang tepat untuk daerah himpunan penyelesaian yang disajikan grafik tersebut adalah ….
S6
Perhatikan gambar berikut.

Sistem pertidaksamaan yang tepat untuk daerah himpunan penyelesaian yang disajikan grafik tersebut adalah ….
S7
Perhatikan gambar berikut.

Sistem pertidaksamaan kuadrat dua variabel yang mempunyai daerah penyelesaian berupa daerah yang diarsir adalah ….
S8
Perhatikan SPtKDV berikut.
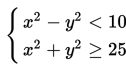
Gambar yang tepat untuk daerah himpunan penyelesaian SPtKDV tersebut adalah ….
S9
Koordinat titik yang merupakan anggota himpunan penyelesaian dari:
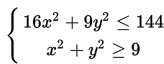
adalah ….
S10
Tinggi Adi 175 cm. Apabila menggunakan tabel BMI berat badan Adi termasuk ideal.

Rumus untuk mendapatkan nilai
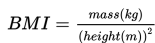
Interval berat badan Adi adalah ….
